题目内容
如图所示,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一点O,使OB=OC,以O为圆心,OB为半径作圆,过C作CO∥AB交⊙O于点D,连接BD。
(1)猜想AC与⊙O的位置关系,并证明你的猜想;
(2)试判断四边形BOCD的形状,并证明你的判断;
(3)已知AC=6,求扇形OBC围成的圆锥的底面圆半径。

解:(1)AC与⊙O相切
 ,∠ACB=120°,∴∠ABC=∠A=30°。
,∠ACB=120°,∴∠ABC=∠A=30°。
 ,∠CBO=∠BCO=30°,
,∠CBO=∠BCO=30°,
∴∠OCA=120°-30°=90°,∴AC⊥OC,
又∵OC是⊙O的半径,
∴AC与⊙O相切。
(2)四边形BOCD是菱形
连接OD。
∵CD∥AB,
∴∠OCD=∠AOC=2×30°=60°
 ,
,
∴△COD是等边三角形,
 ,
,
∴四边形BOCD是平行四边形,

∴四边形BOCD是菱形。
(3)在Rt△AOC中,∠A=30°,AC=6,
 ACtan∠A=6tan30°=
ACtan∠A=6tan30°= ,
,
∴弧BC的弧长
∴底面圆半径

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
下面的图形中,既是轴对称图形又是中心对称图形的是
| | A. |
| B. |
| C. |
| D. |
|
 的解是
的解是 B.
B. C.
C. D.
D.
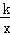 的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为 .
的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为 .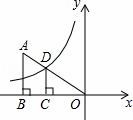
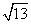 ,则点P的坐标为__________。
,则点P的坐标为__________。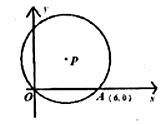
 ,在-1,1,0,2四个数中选一个你喜欢的数,代入求值。
,在-1,1,0,2四个数中选一个你喜欢的数,代入求值。




 中自变量x的取值范围是________,
中自变量x的取值范围是________,