题目内容
如图,△ABC是等边三角形,BD是中线,P是直线BC上一点.(1) 若CP=CD,求证:△DBP是等腰三角形;(2) 在图①中建立以△ABC的边BC的中点为原点,BC所在直线为x轴,BC边上的高所在直线为y轴的平面直角坐标系,如图②,已知等边△ABC的边长为2,AO=![]() ,在x轴上是否存在除点P以外的点Q,使△BDQ是等腰三角形?如果存在,请求出Q点的坐标;如果不存在,请说明理由.
,在x轴上是否存在除点P以外的点Q,使△BDQ是等腰三角形?如果存在,请求出Q点的坐标;如果不存在,请说明理由.

.证明:∵△ABC是等边三角形 ∴∠ABC=∠ACB=60° ∵BD是中线 ∴∠DBC=30°
∵CP=CD ∴∠CPD=∠CDP 又∵∠ACB=60°∴∠CPD=30°∴∠CPD=∠DBC
 ∴DB=DP即△DBP是等腰三角形.
∴DB=DP即△DBP是等腰三角形.
(2) 解:在x轴上存在除点P以外的点Q,使△BDQ是等腰三角形
①若点P在x轴负半轴上,且BP=BD ∵BD= ∴BP=
∴BP=![]()
∴OP= ∴点P1(
∴点P1(![]() ,0)②若点P在x轴上,且BP=PD
,0)②若点P在x轴上,且BP=PD
∵∠PBD=∠PDB=30° ∴∠DPC=60°又∠PCD=60°∴PC=DC=1
而OC=1 ∴OP=0 ∴点P2(0,0)
③若点P在x轴正半轴上,且BP=BD ∴BP= 而OB=1
而OB=1
∴OP= ∴点P3(
∴点P3(![]() ,0)
,0)
解析:略

练习册系列答案
相关题目
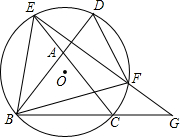 ∥AC,EF的延长线交BC的延长线于点G.
∥AC,EF的延长线交BC的延长线于点G. 9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角
9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角 如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于
如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于 如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是
如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.