题目内容
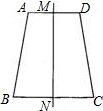 如图,已知一等腰梯形,其底为a和b,高为h
如图,已知一等腰梯形,其底为a和b,高为h
(1)在梯形的对称轴上求作点P,使从点P看两腰的视角为直角;
(2)求点P到两底边的距离;
(3)在什么条件下可作出P点?
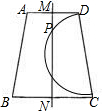 解:(1)以CD为直径做半圆交MN与点P,即为所求;
解:(1)以CD为直径做半圆交MN与点P,即为所求;(2)设P到BC的距离为PN=x,
则:CD2=PD2+PC2=(MD2+MP2)2+(PN2+NC2)=
 +(h-x)2+x2+
+(h-x)2+x2+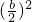 ,
,又CD2=MN2+
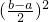 =h2+
=h2+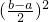 ,
,∴
 +(h-x)2+x2+
+(h-x)2+x2+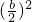 =h2+
=h2+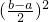 .
.整理得4x2-4hx+ab=0,
解得:PM=x=
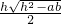 ;
;(3)求作P点的作图是否可以实现,显然取决于方程4x2-4hx+ab=0是否有实数解,
即取决于△=16(h2-ab),
当h2>ab时,△>0,即可以作出两点,
当h2=ab时,△=0,即可以作出一点,
当h2<ab时,△<0,作圆不能实现.
分析:(1)从点P看两腰的视角为直角即∠DPC为直角即P在以CD为直径的圆上;
(2)可设P到BC的距离为PN=x,在△CDP中,CD2=PD2+PC2,由勾股定理可求出P到BC底边的距离;
(3)P点的作图是否可以实现,显然取决于方程4x2-4hx+ab=0是否有实数解,即取决于△=16(h2-ab),
点评:本题主要考查了等腰梯形的性质,难度较大,关键将问题与圆结合,利用圆的性质特点解决问题.

练习册系列答案
相关题目

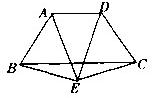 (1)如图,已知等腰梯形ABCD中,AB=CD,AD∥BC,E是梯形外一点,且EA=ED,求证:EB=EC
(1)如图,已知等腰梯形ABCD中,AB=CD,AD∥BC,E是梯形外一点,且EA=ED,求证:EB=EC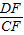 的值.
的值.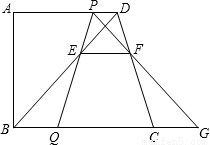
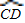 的中点,连接PD、PA、PB、PC,
的中点,连接PD、PA、PB、PC,