题目内容
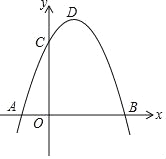
【题目】如图,抛物线y=﹣x2+bx+c过点B(3,0),C(0,3),D为抛物线的顶点.
(1)求抛物线的解析式以及顶点坐标;
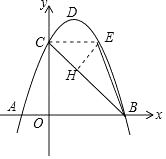
(2)点C关于抛物线y=﹣x2+bx+c对称轴的对称点为E点,联结BC,BE,求∠CBE的正切值;
(3)点M是抛物线对称轴上一点,且△DMB和△BCE相似,求点M坐标.
【答案】(1)y=﹣x2+2x+3,(1,4);(2)![]() ;(3)(1,
;(3)(1,![]() )或(1,﹣2).
)或(1,﹣2).
【解析】
试题分析:(1)利用待定系数法求出二次函数的解析式,根据二次函数的性质解答即可;
(2)过点E作EH⊥BC于点H,根据轴对称的性质求出点E的坐标,根据三角形的面积公式求出EH、BH,根据正切的定义计算即可;
(3)分![]() 和
和![]() 两种情况,计算即可.
两种情况,计算即可.
试题解析:(1)∵抛物线y=﹣x2+bx+c经过点B(3,0)和点C(0,3)
∴![]() ,
,
解得![]() ,
,
∴抛物线解析式为y=﹣x2+2x+3,
y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线顶点D的坐标为(1,4),
(2)由(1)可知抛物线对称轴为直线x=1,
∵点E与点C(0,3)关于直线x=1对称,
∴点E(2,3),
过点E作EH⊥BC于点H,
∵OC=OB=3,
∴BC=![]() ,
,
∵![]() ,CE=2,
,CE=2,
∴![]() ,
,
解得EH=![]() ,
,
∵∠ECH=∠CBO=45°,
∴CH=EH=![]() ,
,
∴BH=2![]() ,
,
∴在Rt△BEH中,![]() ;
;
(3)当点M在点D的下方时
设M(1,m),对称轴交x轴于点P,则P(1,0),
∴BP=2,DP=4,
∴![]() ,
,
∵![]() ,∠CBE、∠BDP均为锐角,
,∠CBE、∠BDP均为锐角,
∴∠CBE=∠BDP,
∵△DMB与△BEC相似,
∴![]() 或
或![]() ,
,
①![]() ,
,
∵DM=4﹣m,![]() ,
,![]() ,
,![]()
∴![]() ,
,
解得,![]() ,
,
∴点M(1,![]() )
)
②![]() ,则
,则![]() ,
,
解得m=﹣2,
∴点M(1,﹣2),
当点M在点D的上方时,根据题意知点M不存在.
综上所述,点M的坐标为(1,![]() )或(1,﹣2).
)或(1,﹣2).

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目