题目内容
如图,Rt△ABC≌Rt△DEC,∠BCA=∠ECD=90°,∠A=∠D=30°,点E是斜边AB上的一点,把△ABC绕点C按 顺时针方向旋转n度后恰好与△DEC重合,AC与DE交于F.
顺时针方向旋转n度后恰好与△DEC重合,AC与DE交于F.
(1)求旋转角度n的值;
(2)若BC=2,①求EF的长; ②求点A所经过的路线的长.
解:(1)∵∠BCA=∠ECD=90°,∠A=∠D=30°,
∴∠BCE=60°,
∵Rt△ABC≌Rt△DEC,
∴旋转角度n的值60;
(2)①∵BC=2,
∴AB=4,
∴AE=CE=2,
∴EF= AE=1,
AE=1,
②点A所经过的路线的长是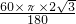 =
= .
.
分析:(1)根据旋转的性质得,CB=CE,再由已知条件可证明△BCE为等边三角形,从而得出旋转角的度数;
(2)①由已知条件得点F平分AC,在直角三角形AEF中,EF= AE,②点A所经过的路线的长是以点C为圆心,以AC为半径,60°扇形的弧长.
AE,②点A所经过的路线的长是以点C为圆心,以AC为半径,60°扇形的弧长.
点评:本题考查了弧长的计算,全等三角形的性质以及旋转的性质,是基础知识要熟练掌握.
∴∠BCE=60°,
∵Rt△ABC≌Rt△DEC,
∴旋转角度n的值60;
(2)①∵BC=2,
∴AB=4,
∴AE=CE=2,
∴EF=
 AE=1,
AE=1,②点A所经过的路线的长是
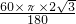 =
= .
.分析:(1)根据旋转的性质得,CB=CE,再由已知条件可证明△BCE为等边三角形,从而得出旋转角的度数;
(2)①由已知条件得点F平分AC,在直角三角形AEF中,EF=
 AE,②点A所经过的路线的长是以点C为圆心,以AC为半径,60°扇形的弧长.
AE,②点A所经过的路线的长是以点C为圆心,以AC为半径,60°扇形的弧长.点评:本题考查了弧长的计算,全等三角形的性质以及旋转的性质,是基础知识要熟练掌握.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目

 如图,Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从B点出发,以2cm/s的速度向点C运动,点Q从C点出发,以1cm/s的速度向点A运动.若P,Q同时出发,则经过
如图,Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从B点出发,以2cm/s的速度向点C运动,点Q从C点出发,以1cm/s的速度向点A运动.若P,Q同时出发,则经过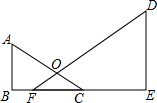 已知,如图,Rt△ABC中∠B=90°,Rt△DEF中∠E=90°,OF=OC,AB=6,BF=2,CE=8,CA=0,DE=15.
已知,如图,Rt△ABC中∠B=90°,Rt△DEF中∠E=90°,OF=OC,AB=6,BF=2,CE=8,CA=0,DE=15. (2013•封开县一模)如图,Rt△ABC的直角边BC=8,AC=6
(2013•封开县一模)如图,Rt△ABC的直角边BC=8,AC=6