��Ŀ����
����Ŀ��![]() ��0��
��0�� ![]() ��
��![]() .
.
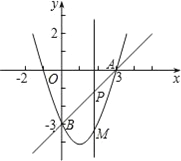
��1���������ߵĽ���ʽ.
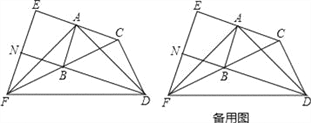
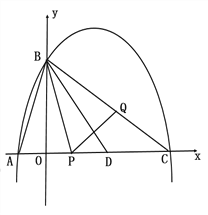
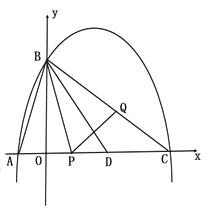
��2����������![]() �ύ����һ������ΪC����D���߶�AC�ϣ���֪AD=AB��������P��A�������߶�AC��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ��һ������Q��ijһ�ٶȴ�B�������߶�BC�����˶������Ƿ����ijһʱ�̣�ʹ�߶�PQ��ֱ��BD��ֱƽ�֣������ڣ������Q���˶��ٶȣ��������ڣ���˵������.
�ύ����һ������ΪC����D���߶�AC�ϣ���֪AD=AB��������P��A�������߶�AC��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ��һ������Q��ijһ�ٶȴ�B�������߶�BC�����˶������Ƿ����ijһʱ�̣�ʹ�߶�PQ��ֱ��BD��ֱƽ�֣������ڣ������Q���˶��ٶȣ��������ڣ���˵������.
��3���ڣ�2����ǰ���£�����B��ֱ��![]() ��
��![]() ��ĸ����ύ�ڵ�M,�Ƿ���ڵ�M,ʹ��A��B��MΪ�������������
��ĸ����ύ�ڵ�M,�Ƿ���ڵ�M,ʹ��A��B��MΪ�������������![]() ����,������ڣ���ֱ��д��M�����ꣻ�������ڣ���˵������.
����,������ڣ���ֱ��д��M�����ꣻ�������ڣ���˵������.
���𰸡���1��![]() ����2�����ڣ���Q���˶��ٶ�ÿ��
����2�����ڣ���Q���˶��ٶ�ÿ��![]() ����λ���ȣ���3�����ڣ�
����λ���ȣ���3�����ڣ� ![]() ��
�� ![]()
�������������������1���������ߵĽ���ʽΪy=a��x-![]() ��2+k��a��0�����ѵ�A��-1,0����B��0��
��2+k��a��0�����ѵ�A��-1,0����B��0�� ![]() �����룬�ⷽ�̼��ɣ�
�����룬�ⷽ�̼��ɣ�
��2���������A��C���꣬�ɡ�DBP=��DBQ���ɵ�![]() ����ƽ���ߵ����ʶ����������������֤��������
����ƽ���ߵ����ʶ����������������֤�������� ���ⷽ�̼�����
���ⷽ�̼�����
��3�����ڣ��������£�����֤����BPC=��BAM��������������ۣ��ٵ�![]() ����MAB�ס�BPC���г����̼��ɣ��ڵ�
����MAB�ס�BPC���г����̼��ɣ��ڵ�![]() ����MAB�ס�CPB���г����̼���.
����MAB�ס�CPB���г����̼���.
�����������1��![]()
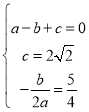
���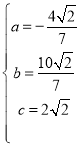
��![]()
��2������DQ,��t��ʱ���߶�PQ��ֱ��BD��ֱƽ��,
��![]()
![]() .
. ![]()
![]()
![]() =AD
=AD
��![]() ,CD=
,CD=![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��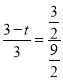
![]()
![]() ,OC=
,OC=![]() ,���ݹ��ɶ����ã�BC=
,���ݹ��ɶ����ã�BC=![]()
��![]()
��![]()
��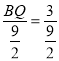
��![]()
![]() ��Q���˶��ٶ�ÿ��
��Q���˶��ٶ�ÿ��![]() ����λ����
�������
��3��![]()
��![]()

����Ŀ����֪ ![]() ��
�� ![]() ��
��
��1���� ![]() ȡ��ֵʱ��
ȡ��ֵʱ�� ![]() ��
��
��2���� ![]() ȡ��ֵʱ��
ȡ��ֵʱ�� ![]() ��ֵ��
��ֵ�� ![]() ��ֵ��3����1��
��ֵ��3����1��
��3�����������ش�
��
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| ||||||||
|
�ڸ���������ش����⣺���� ![]() ��ֵ����
��ֵ���� ![]() ��ֵ�� ��
��ֵ�� �� ![]() ��ֵ�� ��
��ֵ�� ��