题目内容
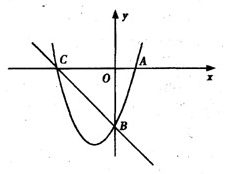
如图,已知抛物线y=a(x-1)2+![]() (a≠0)经过点A(-2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点D平行于
(a≠0)经过点A(-2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点D平行于![]() 轴的直线交射线OM于点C,B在
轴的直线交射线OM于点C,B在![]() 轴正半轴上,连结BC.
轴正半轴上,连结BC.
(1)求该抛物线的解析式;
(2)①若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为t(s).问:当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?
②若OC=OB,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t(s),连接PQ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时PQ的长.

解:(1)把A(-2,0)代入y=a(x-1)2+![]() ,得0=a(-2-1)2+
,得0=a(-2-1)2+![]() .
.
∴a=-![]() ···························· 1分
···························· 1分
∴该抛物线的解析式为y=-![]() (x-1)2+
(x-1)2+![]()
即y=-![]() x 2+
x 2+![]() x+
x+![]() .···················· 3分
.···················· 3分
(2)设点D的坐标为(xD,yD),由于D为抛物线的顶点
∴xD=- =1,yD=-
=1,yD=-![]() ×1 2+
×1 2+![]() ×1+
×1+![]() =
=![]() .
.
∴点D的坐标为(1,![]() ).
).
如图,过点D作DN⊥x轴于N,则DN=![]() ,AN=3,∴AD=
,AN=3,∴AD=![]() =6.
=6.

∴∠DAO=60°·························· 4分
∵OM∥AD
①当AD=OP时,四边形DAOP为平行四边形.
∴OP=6
∴t=6(s)··················· 5分
②当DP⊥OM时,四边形DAOP为直角梯形.
过点O作OE⊥AD轴于E.
在Rt△AOE中,∵AO=2,∠EAO=60°,∴AE=1.
(注:也可通过Rt△AOE∽Rt△AND求出AE=1)
∵四边形DEOP为矩形,∴OP=DE=6-1=5.
∴t=5(s)··························· 6分
③当PD=OA时,四边形DAOP为等腰梯形,此时OP=AD-2AE=6-2=4.
∴t=4(s)
综上所述,当t=6s、5s、4s时,四边形DAOP分别为平行四边形、直角梯形、等腰梯形.
·························· 7分
(3)∵∠DAO=60°,OM∥AD,∴∠COB=60°.
又∵OC=OB,∴△COB是等边三角形,∴OB=OC=AD=6.
∵BQ=2t,∴OQ=6-2t(0<t<3)
过点P作PF⊥x轴于F,则PF=![]() t.··············· 8分
t.··············· 8分
∴S四边形BCPQ =S△COB -S△POQ
=![]() ×6×
×6×![]() -
-![]() ×(6-2t)×
×(6-2t)×![]() t
t
=![]() (t-
(t-![]() )2+
)2+![]() ·················· 9分
·················· 9分
∴当t=![]() (s)时,S四边形BCPQ的最小值为
(s)时,S四边形BCPQ的最小值为![]() .··········· 10分
.··········· 10分
此时OQ=6-2t=6-2×![]() =3,OP=
=3,OP=![]() ,OF=
,OF=![]() ,∴QF=3-
,∴QF=3-![]() =
=![]() ,PF=
,PF=![]() .
.
∴PQ=![]() =
=![]() =
=![]() ············ 11分
············ 11分