题目内容
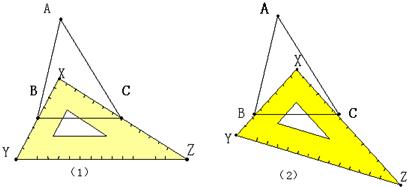
26、(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C、△ABC中,∠A=40°,则∠ABC+∠ACB=
(2)如图2,改变(1)中直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小;
(3)如果(1)中的其它条件不变,把“∠A=40°”改成“∠A=n°”,请直接写出∠ABX+∠ACX的大小.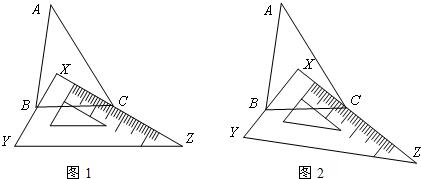
140
度,∠XBC+∠XCB=90
度;(2)如图2,改变(1)中直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小;
(3)如果(1)中的其它条件不变,把“∠A=40°”改成“∠A=n°”,请直接写出∠ABX+∠ACX的大小.

分析:(1)在△ABC中,利用三角形内角和等于180°,可求∠ABC+∠ACB=180°-∠A,即可求∠ABC+∠ACB;同理在△XBC中,∠BXC=90°,那么∠XBC+∠XCB=180°-∠BXC,即可求∠XBC+∠XCB;
(2)不发生变化,由于在△ABC中,∠A=40°,从而∠ABC+∠ACB是一个定值,即等于140°,同理在△XBC中,∠BXC=90°,那么∠XBC+∠XCB也是一个定值,等于90°,于是∠ABX+∠ACX的值不变,等于140°-90°=50°;
(3)利用∠ABX+∠ACX=(∠ABC+∠ACB)-(∠XBC+∠XCB),把具体数值代入,化简即可求出.
(2)不发生变化,由于在△ABC中,∠A=40°,从而∠ABC+∠ACB是一个定值,即等于140°,同理在△XBC中,∠BXC=90°,那么∠XBC+∠XCB也是一个定值,等于90°,于是∠ABX+∠ACX的值不变,等于140°-90°=50°;
(3)利用∠ABX+∠ACX=(∠ABC+∠ACB)-(∠XBC+∠XCB),把具体数值代入,化简即可求出.
解答:解:(1)140°,90°.
(2)不发生变化.
∵∠A=40°,
∴∠ABC+∠ACB=180°-∠A=140°,(三角形内角和180°)
∵∠YXZ=90°,
∴∠XBC+∠XCB=90°,(三角形内角和180°)
∴∠ABX+∠ACX=140°-90°=50°,
(3)90°-n°.
(2)不发生变化.
∵∠A=40°,
∴∠ABC+∠ACB=180°-∠A=140°,(三角形内角和180°)
∵∠YXZ=90°,
∴∠XBC+∠XCB=90°,(三角形内角和180°)
∴∠ABX+∠ACX=140°-90°=50°,
(3)90°-n°.
点评:本题利用了三角形内角和定理.
三角形三个内角的和等于180°.
三角形三个内角的和等于180°.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
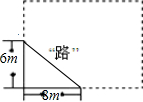 如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了
如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 23、如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.
23、如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积. 如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将其阴影部分进行绿化,中间正方形部分将修建一座雕塑,正方形的边长是(a+b)米.
如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将其阴影部分进行绿化,中间正方形部分将修建一座雕塑,正方形的边长是(a+b)米.