题目内容
如图，直线l1：y=x+1与直线l2：y=-x-
把平面直角坐标系分成四个部分，点（-1，2）在
- A.第一部分
- B.第二部分
- C.第三部分
- D.第四部分
B
分析：先求出两直线的交点坐标，再把所求点与交点位置相比较即可．
解答：设直线l1与直线l2的交点坐标为（x，y），
由题意可得：
，解得：
，
∵-1＜-
，将-1代入y=-x-，y=＜2，∴点（-1，2）在第二部分
方法2：将x=-1分别代入y=x+1，y=-x-得y1=0，y2=，又2＞y2＞y1，所以在第二部分．
故选B．
点评：本题考查了两条直线相交或平行问题，难度不大，关键先求出两直线的交点坐标．
分析：先求出两直线的交点坐标，再把所求点与交点位置相比较即可．
解答：设直线l1与直线l2的交点坐标为（x，y），
由题意可得：
，解得：，∵-1＜-
，将-1代入y=-x-，y=＜2，∴点（-1，2）在第二部分方法2：将x=-1分别代入y=x+1，y=-x-
得y1=0，y2=，又2＞y2＞y1，所以在第二部分．故选B．
点评：本题考查了两条直线相交或平行问题，难度不大，关键先求出两直线的交点坐标．
练习册系列答案
相关题目
20、如图，直线l1：y=x+1与直线l2：y=mx+n相交于点P（a，3），则关于x的不等式x+1≥mx+n的解集为
如图，直线l1、l2交于点A，试求点A的坐标．
如图，直线l1：y=2x+4与l2：y=-x-5在同一平面角坐标系中相交于点P，则点P的坐标是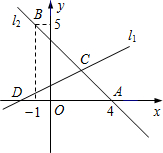
l2交于点C．
如图，直线l1，l2交于点A，直线l2与x轴交于点B，与y轴交于点D，直线l1所对应的函数关系式为y=-2x+2．