题目内容
如图,点A(2,6)和点B(点B在点A的右侧)在反比例函数的图像上,点C在![]() 轴上,BC//
轴上,BC//![]() 轴,
轴,![]() ,二次函数的图像经过A、B、C三点.
,二次函数的图像经过A、B、C三点.
(1) 求反比例函数和二次函数的解析式;
(2) 如果点D在![]() 轴的正半轴上,点E在反比例函数的图像上,四边形ACDE是平行四边形,求边CD的长.
轴的正半轴上,点E在反比例函数的图像上,四边形ACDE是平行四边形,求边CD的长.
![]()
 |
解:(1)设反比例函数的解析式为![]() .
.
![]() ∵点A(2,6)在反比例函数的图像上,∴6=
∵点A(2,6)在反比例函数的图像上,∴6=![]() ,
,
∴![]() ,∴反比例函数的解析式为
,∴反比例函数的解析式为![]() .
.
作AM⊥BC,垂足为M,交![]() 轴于N,∴CM=2.
轴于N,∴CM=2.
在Rt△ACM中,![]() .
.
∵BC//![]() 轴,OC=
轴,OC=![]() AN–AM=6–4=2,∴点
AN–AM=6–4=2,∴点![]() C的坐标(0,2).
C的坐标(0,2).
当![]() 时,
时,![]() ,∴点B的坐标(6,2)
,∴点B的坐标(6,2)
设二次函数的解析式为![]() ,
,![]()
∴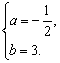 ∴二次函数的解析式为
∴二次函数的解析式为![]() .
.
(2)延长AC交![]() 轴于G,作EH⊥
轴于G,作EH⊥![]() 轴,垂足为H.
轴,垂足为H.
∵在□ACDE中,AC//DE,∴∠AGO=∠EDH.
∵BC//![]() 轴,∴∠ACM=∠AGO.∴∠ACM=∠EDH.
轴,∴∠ACM=∠AGO.∴∠ACM=∠EDH.
∵∠AMC=∠EHD=90º,AC=ED,∴△ACM≌△EDH.
∴EH=AM=4,DH=CM=2.∴点E(3,4).
∴OE=3,OD=OE–DH=1
∴CD=![]() .
.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 如图,点A的坐标为(2
如图,点A的坐标为(2| 2 |
| A、(0,0) | ||||||||
B、(
| ||||||||
| C、(1,1) | ||||||||
D、(
|

 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°.
 12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是
12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是