Question

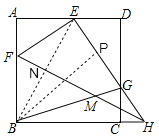
【题目】正方形ABCD中，F是AB上一点，H是BC延长线上一点，连接FH，将△FBH沿FH翻折，使点B的对应点E落在AD上，EH与CD交于点G，连接BG交FH于点M，当GB平分∠CGE时，BM=，AE=8，则S四边形EFMG=________．

Answer 1

【答案】

【解析】解：过B作BP⊥EH于P，连接BE，交FH于N，则∠BPG=90°，∵四边形ABCD是正方形，∴∠BCD=∠ABC=∠BAD=90°，AB=BC，∴∠BCD=∠BPG=90°，∵∠EGB=∠CGB，BG=BG，∴△BPG≌△BCG，∴∠PBG=∠CBG，BP=BC，∴AB=BP，∵∠BAE=∠BPE=90°，BE=BE，∴Rt△ABE≌Rt△PBE（HL），∴∠ABE=∠PBE，∴∠EBG=∠EBP+∠GBP=∠ABC=45°，由折叠得：BF=EF，BH=EH，∴FH垂直平分BE，∴△BNM是等腰直角三角形，∵BM=，∴BN=NM==，∴BE=，∵AE=8，∴DE=12﹣8=4，由勾股定理得：AB===12，设BF=x，则EF=x，AF=12﹣x，由勾股定理得：x2=82+（12﹣x）2，x=，∴BF=EF=，∵△ABE≌△PBE，∴EP=AE=8，BP=AB=12，同理可得：PG=，Rt△EFN中，FN=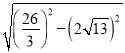 =，∴S四边形EFMG=S△EFN+S△EBG﹣S△BNM=FNEN+EGBP﹣BNNM=××+（8+）×12﹣××=．故答案为： ．