题目内容
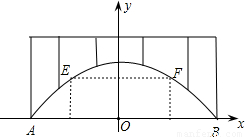
如图，是某座抛物线型桥的示意图，已知抛物线的函数表达式为
，为保护桥的安全，在该抛物线上距水面AB高为8.5米的点E、F处要安装两盏警示灯，则这两盏灯的水平距离EF是 米（结果保留根号）．
【答案】分析：由抛物线的解析式为
，令y=8.5，求得E、F两点的横坐标作差即可．
解答：解：点E、F距离AB高为8.5米，所以点E、F的纵坐标都是8.5，
把y=8.5代入函数表达式得出：
，
，
x2=1.5×36=54，
；
∵EF大于0，
∴根据抛物线关于对称轴的轴对称性质，则有：EF=
米．
点评：本题考查了二次函数在实际生活中的运用，代入点的纵坐标求横坐标，较为简单．
，令y=8.5，求得E、F两点的横坐标作差即可．解答：解：点E、F距离AB高为8.5米，所以点E、F的纵坐标都是8.5，
把y=8.5代入函数表达式得出：
，，x2=1.5×36=54，
；∵EF大于0，
∴根据抛物线关于对称轴的轴对称性质，则有：EF=
米．点评：本题考查了二次函数在实际生活中的运用，代入点的纵坐标求横坐标，较为简单．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
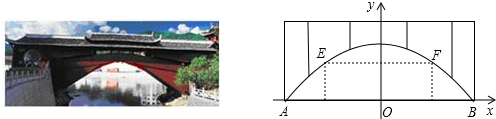
如图，是某座抛物线型桥的示意图，已知抛物线的函数表达式为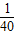
x2+10，为保护廊桥的安全，在该抛物线上距水面AB高为8米的点E，F处要安装两盏警示灯，则这两盏灯的水平距离EF是 米．（精确到1米）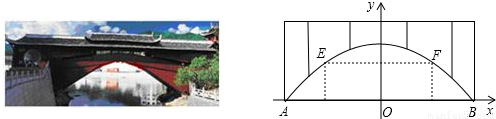
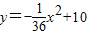，为保护桥的安全，在该抛物线上距水面AB高为8.5米的点E、F处要安装两盏警示灯，则这两盏灯的水平距离EF是 米（结果保留根号）．