题目内容
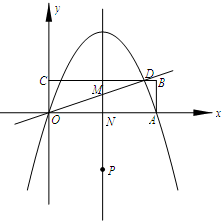 矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(10,0)、C(0,3),直线
矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(10,0)、C(0,3),直线 与BC相交于点D,抛物线y=ax2+bx经过A、D两点.
与BC相交于点D,抛物线y=ax2+bx经过A、D两点.
(1)求抛物线的解析式;
(2)连接AD,试判断△OAD的形状,并说明理由.
(3)若点P是抛物线的对称轴上的一个动点,对称轴与OD、x轴分别交于点M、N,问:是否存在点P,使得以点P、O、M为顶点的三角形与△OAD相似?若存在,请求出点P的坐标;若不存在,请说明理由.
解:(1)由题意得,点D的纵坐标为3,
∵点D在直线y= x上,
x上,
∴点D的坐标为(9,3),
将点D(9,3)、点A(10,0)代入抛物线可得: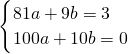 ,
,
解得: ,
,
故抛物线的解析式为:y=- x2+
x2+ x.
x.
(2)∵点D坐标为(9,3),点A坐标为(10,0),
∴OA=10,OD=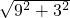 =3
=3 ,AD=
,AD=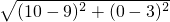 =
= ,
,
从而可得OA2=OD2+AD2,
故可判断△OAD是直角三角形.
(3)①由图形可得当点P和点N重合时能满足△OPM∽△ODA,
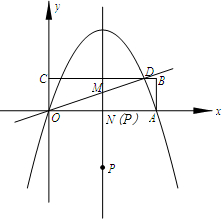
此时∠POM=∠DOA,∠OPM=∠ODA,
故可得△OPM∽△ODA,OP= OA=5,
OA=5,
即可得此时点P的坐标为(5,0).
②过点O作OD的垂线交对称轴于点P′,此时也可满足△P′OM∽△ODA,
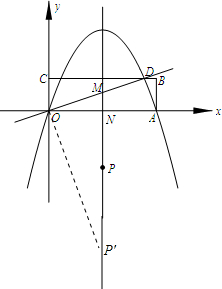
由题意可得,点M的横坐标为5,代入直线方程可得点M的纵坐标为 ,
,
故可求得OM=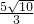 ,
,
∵∠OP′M+∠OMN=∠DOA+∠OMN=90°,
∴∠OP′M=∠DOA,
∴△P′OM∽△ODA,
故可得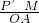 =
=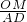 ,即
,即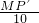 =
=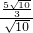 ,
,
解得:MP′= ,
,
又∵MN=点M的纵坐标= ,
,
∴P′N= -
- =15,
=15,
即可得此时点P′的坐标为(5,-15).
综上可得存在这样的点P,点P的坐标为(5,0)或(5,-15).
分析:(1)根据题意可得出点D的纵坐标为3,代入直线解析式可得出点D的横坐标,从而将点D和点A的坐标代入可得出抛物线的解析式.
(2)分别求出OA、OD、AD的长度,继而根据勾股定理的逆定理可判断出△OAD是直角三角形.
(3)①由图形可得当点P和点N重合时能满足△OPM∽△ODA,②过点O作OD的垂线交对称轴于点P′,此时也可满足△P′OM∽△ODA,利用相似的性质分别得出点P的坐标即可.
点评:此题考查了二次函数的综合题,解答本题的关键是结合直线解析式求出点D的坐标,得出抛物线的解析式,在第三问的解答中要分类讨论,不要漏解.
∵点D在直线y=
 x上,
x上,∴点D的坐标为(9,3),
将点D(9,3)、点A(10,0)代入抛物线可得:
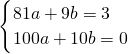 ,
,解得:
 ,
,故抛物线的解析式为:y=-
 x2+
x2+ x.
x.(2)∵点D坐标为(9,3),点A坐标为(10,0),
∴OA=10,OD=
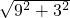 =3
=3 ,AD=
,AD=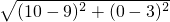 =
= ,
,从而可得OA2=OD2+AD2,
故可判断△OAD是直角三角形.
(3)①由图形可得当点P和点N重合时能满足△OPM∽△ODA,

此时∠POM=∠DOA,∠OPM=∠ODA,
故可得△OPM∽△ODA,OP=
 OA=5,
OA=5,即可得此时点P的坐标为(5,0).
②过点O作OD的垂线交对称轴于点P′,此时也可满足△P′OM∽△ODA,

由题意可得,点M的横坐标为5,代入直线方程可得点M的纵坐标为
 ,
,故可求得OM=
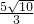 ,
,∵∠OP′M+∠OMN=∠DOA+∠OMN=90°,
∴∠OP′M=∠DOA,
∴△P′OM∽△ODA,
故可得
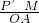 =
=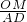 ,即
,即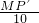 =
=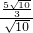 ,
,解得:MP′=
 ,
,又∵MN=点M的纵坐标=
 ,
,∴P′N=
 -
- =15,
=15,即可得此时点P′的坐标为(5,-15).
综上可得存在这样的点P,点P的坐标为(5,0)或(5,-15).
分析:(1)根据题意可得出点D的纵坐标为3,代入直线解析式可得出点D的横坐标,从而将点D和点A的坐标代入可得出抛物线的解析式.
(2)分别求出OA、OD、AD的长度,继而根据勾股定理的逆定理可判断出△OAD是直角三角形.
(3)①由图形可得当点P和点N重合时能满足△OPM∽△ODA,②过点O作OD的垂线交对称轴于点P′,此时也可满足△P′OM∽△ODA,利用相似的性质分别得出点P的坐标即可.
点评:此题考查了二次函数的综合题,解答本题的关键是结合直线解析式求出点D的坐标,得出抛物线的解析式,在第三问的解答中要分类讨论,不要漏解.

练习册系列答案
相关题目
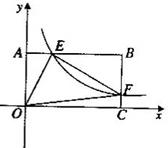

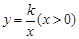 的图象与边BC交于点F。
的图象与边BC交于点F。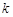 的值:
的值:
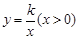 的图象与边BC交于点F。
的图象与边BC交于点F。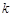 的值:
的值:
 的图象与边BC交于点F.
的图象与边BC交于点F.
 .且
.且 ,求k的值.
,求k的值.