题目内容
如图10-1,在平面直角坐标系 中,点
中,点 在
在 轴的正半轴上, ⊙
轴的正半轴上, ⊙ 交
交 轴于
轴于  两点,交
两点,交 轴于
轴于 两点,且
两点,且 为
为 的中点,
的中点, 交
交 轴于
轴于 点,若点
点,若点 的坐标为(-2,0),
的坐标为(-2,0),


(1)(3分)求点
 的坐标.
的坐标. (2)(3分)连结
 ,求证:
,求证: ∥
∥
(3)(4分) 如图10-2,过点
 作⊙
作⊙ 的切线,交
的切线,交 轴于点
轴于点 .动点
.动点 在⊙
在⊙ 的圆周上运动时,
的圆周上运动时, 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
(1)(0,4)
(2)证明略
(3)
 解析:
解析:解(1)方法(一)∵直径AB⊥CD
∴CO=
 CD ……1分
CD ……1分 =
=
∵C为
 的中点
的中点∴
 =
=
∴
 =
=
∴CD=AE ……2分
∴CO=
 CD=4
CD=4∴C点的坐标为(0,4) ……3分
方法(二)连接CM,交AE于点N
∵C为
 的中点,M为圆心
的中点,M为圆心∴AN=
 AE=4 ……1分
AE=4 ……1分CM⊥AE
∴∠ANM=∠COM=90°
在△ANM和△COM中:

∴△ANM≌△COM ……2分
∴CO=AN=4
∴C点的坐标为(0,4) ……3分
解(2)设半径AM=CM=r,则OM=r-2
由OC
 +OM
+OM =MC
=MC 得:
得:4
 +(r-2)
+(r-2) =r
=r
解得:r=5 ……1分
∵∠AOC=∠ANM=90°
∠EAM=∠MAE
∴△AOG∽△ANM
∴

∵MN=OM=3
即

∴OG=
 ……2分
……2分∵


∴

∵∠BOC=∠BOC
∴△GOM∽△COB
∴∠GMO=∠CBO
∴MG∥BC ……3分
(说明:直接用平行线分线段成比例定理的逆定理不扣分)
解(3)连结DM,则DM⊥PD,DO⊥PM
∴△MOD∽△MDP,△MOD∽△DOP
∴DM
 =MO·MP;
=MO·MP;DO
 =OM·OP(说明:直接使用射影定理不扣分)
=OM·OP(说明:直接使用射影定理不扣分)即4
 =3·OP
=3·OP∴OP=
 ……1分
……1分当点F与点A重合时:

当点F与点B重合时:
 ……2分
……2分当点F不与点A、B重合时:连接OF、PF、MF
∵DM
 =MO·MP
=MO·MP∴FM
 =MO·MP
=MO·MP∴

∵∠AMF=∠FMA
∴△MFO∽△MPF
∴

∴综上所述,
 的比值不变,比值为
的比值不变,比值为 ……4分
……4分 
练习册系列答案
相关题目
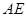
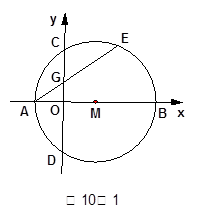
 中,点
中,点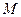 在
在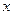 轴的正半轴上, ⊙
轴的正半轴上, ⊙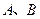 两点,交
两点,交 轴于
轴于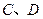 两点,且
两点,且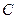 为
为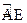 的中点,
的中点,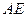 交
交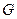 点,若点
点,若点 的坐标为(-2,0),
的坐标为(-2,0),

 ,求证:
,求证: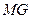 ∥
∥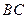
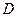 作⊙
作⊙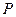 .动点
.动点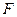 在⊙
在⊙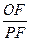 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律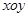 中,点
中,点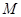 在
在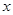 轴的正半轴上,
⊙
轴的正半轴上,
⊙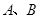 两点,交
两点,交 轴于
轴于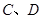 两点,且
两点,且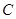 为
为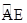 的中点,
的中点, 交
交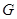 点,若点
点,若点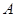 的坐标为(-2,0),
的坐标为(-2,0),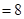
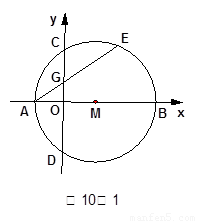
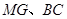 ,求证:
,求证: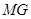 ∥
∥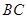
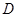 作⊙
作⊙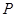 .动点
.动点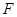 在⊙
在⊙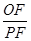 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律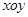 中,点
中,点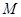 在
在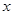 轴的正半轴上, ⊙
轴的正半轴上, ⊙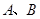 两点,交
两点,交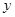 轴于
轴于 两点,且
两点,且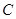 为
为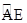 的中点,
的中点,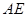 交
交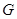 点,若点
点,若点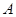 的坐标为(-2,0),
的坐标为(-2,0),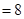
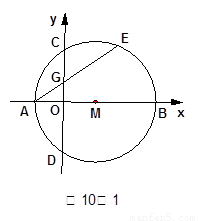
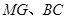 ,求证:
,求证: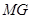 ∥
∥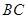
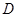 作⊙
作⊙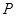 .动点
.动点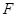 在⊙
在⊙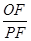 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律