题目内容
如果四边形一条对角线所在直线上有一点,它到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这个点为这个四边形的准等距点.
(1)正方形ABCD的对角线AC上有没有准等距点?请简单说明理由;
(2)请回答长方形(正方形除外)、菱形、等腰梯形的准等距点的个数(不必证明);
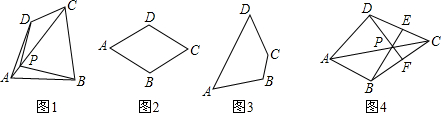
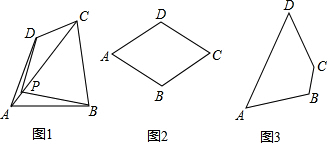
(3)如图所示,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF,证明点P是四边形ABCD的准等距点.
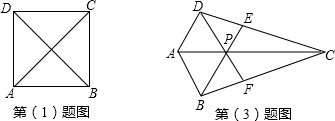
(1)正方形ABCD的对角线AC上有没有准等距点?请简单说明理由;
(2)请回答长方形(正方形除外)、菱形、等腰梯形的准等距点的个数(不必证明);
(3)如图所示,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF,证明点P是四边形ABCD的准等距点.

分析:(1)如图1,在对角线AC上任取一点P,连接PB,PD,根据正方形的性质就可以得出PD=PB,就可以得出结论;
(2)由矩形的对角线互相平分但不垂直,就可以得出矩形的准等距点的个数为0,菱形的对角线互相垂直平分,可以得出菱形的准等距点的个数是无数个,等腰梯形不垂直又不互相平分,且任何一条对角线的中垂线都不经过另一条对角线的中点,可以得出等腰梯形的准等距点的个数为2个;
(3)根据条件可以得出△CDF≌△CBE就可以得出BC=DC,进而可以得出BF=DE,再证明△EDP≌△FBP就可以得出PD=PB就可以得出结论.
(2)由矩形的对角线互相平分但不垂直,就可以得出矩形的准等距点的个数为0,菱形的对角线互相垂直平分,可以得出菱形的准等距点的个数是无数个,等腰梯形不垂直又不互相平分,且任何一条对角线的中垂线都不经过另一条对角线的中点,可以得出等腰梯形的准等距点的个数为2个;
(3)根据条件可以得出△CDF≌△CBE就可以得出BC=DC,进而可以得出BF=DE,再证明△EDP≌△FBP就可以得出PD=PB就可以得出结论.
解答:解:(1)如图1,在对角线AC上任取一点P,连接PB,PD.
∵四边形ABCD是正方形,
∴BD⊥AC,AC平分BD,
∴PD=PB.
∴点P是对角线AC上的准等距点;
(2)根据确定准等距点的方法:可以作出其中一条对角线的垂直平分线和另一条对角线所在的直线的交点.主要是根据两条对角线的位置关系决定.
∵矩形的对角线互相平分但不垂直,
∴矩形的准等距点的个数为0,
∵菱形的对角线互相垂直平分,
∴菱形的准等距点的个数是无数个,
∵等腰梯形不垂直又不互相平分,且任何一条对角线的中垂线都不经过另一条对角线的中点,
∴等腰梯形的准等距点的个数为2个;
(3)在△CDF和△CBE中,
,
∴△CDF≌△CBE(AAS),
∴CD=CB.
∵CE=CF,
∴ED=BF.
在△EDP和△FBP中,
,
∴△EDP≌△FBP(AAS),
∴PD=PB.
∴点P是四边形ABCD的准等距点.

∵四边形ABCD是正方形,
∴BD⊥AC,AC平分BD,
∴PD=PB.
∴点P是对角线AC上的准等距点;
(2)根据确定准等距点的方法:可以作出其中一条对角线的垂直平分线和另一条对角线所在的直线的交点.主要是根据两条对角线的位置关系决定.
∵矩形的对角线互相平分但不垂直,
∴矩形的准等距点的个数为0,
∵菱形的对角线互相垂直平分,
∴菱形的准等距点的个数是无数个,
∵等腰梯形不垂直又不互相平分,且任何一条对角线的中垂线都不经过另一条对角线的中点,
∴等腰梯形的准等距点的个数为2个;
(3)在△CDF和△CBE中,
|
∴△CDF≌△CBE(AAS),
∴CD=CB.
∵CE=CF,
∴ED=BF.
在△EDP和△FBP中,
|
∴△EDP≌△FBP(AAS),
∴PD=PB.
∴点P是四边形ABCD的准等距点.
点评:本考查了菱形的性质、全等三角形的判定与性质、线段垂直平分线的性质等知识.此题属于阅读性题目,解题的关键是熟悉垂直平分线的性质,能够根据找准等距点的方和四边形中两条对角线的位置关系判断准等距点的个数及证明一个点是四边形的准等距点.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目