题目内容
 在如图所示的网格中,△MNP绕某点旋转一定角度,得到△M1N1P1,其旋转中心可能是
在如图所示的网格中,△MNP绕某点旋转一定角度,得到△M1N1P1,其旋转中心可能是
- A.点A
- B.点B
- C.点C
- D.点D
A
分析:观察图形可得到B点到M与M1的距离不相等,C点到N与N1的距离不相等,D点到P与P1的距离不相等,则点B、C、D不可能为旋转中心;连AM、AN、AP、AM1、AN1、AP1,利用勾股定理易得AP=AP1= ,AM=AM1=
,AM=AM1= ,AN=AN1=
,AN=AN1= ,并且∠PAP1=∠MAM1=∠NAN1=180°,于是可判断旋转中心为点A.
,并且∠PAP1=∠MAM1=∠NAN1=180°,于是可判断旋转中心为点A.
解答: 连AM、AN、AP、AM1、AN1、AP1,如图,设网格中每个小正方形的边长为1,
连AM、AN、AP、AM1、AN1、AP1,如图,设网格中每个小正方形的边长为1,
则AP=AP1= ,AM=AM1=
,AM=AM1= ,AN=AN1=
,AN=AN1= ,∠PAP1=∠MAM1=∠NAN1=180°,
,∠PAP1=∠MAM1=∠NAN1=180°,
所以△MNP可看作绕点A旋转°180,得到△M1N1P1.
故选A.
点评:本题考查了旋转的性质:旋转前后两图形全等,即对应线段相等,对应角相等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.
分析:观察图形可得到B点到M与M1的距离不相等,C点到N与N1的距离不相等,D点到P与P1的距离不相等,则点B、C、D不可能为旋转中心;连AM、AN、AP、AM1、AN1、AP1,利用勾股定理易得AP=AP1=
 ,AM=AM1=
,AM=AM1= ,AN=AN1=
,AN=AN1= ,并且∠PAP1=∠MAM1=∠NAN1=180°,于是可判断旋转中心为点A.
,并且∠PAP1=∠MAM1=∠NAN1=180°,于是可判断旋转中心为点A.解答:
 连AM、AN、AP、AM1、AN1、AP1,如图,设网格中每个小正方形的边长为1,
连AM、AN、AP、AM1、AN1、AP1,如图,设网格中每个小正方形的边长为1,则AP=AP1=
 ,AM=AM1=
,AM=AM1= ,AN=AN1=
,AN=AN1= ,∠PAP1=∠MAM1=∠NAN1=180°,
,∠PAP1=∠MAM1=∠NAN1=180°,所以△MNP可看作绕点A旋转°180,得到△M1N1P1.
故选A.
点评:本题考查了旋转的性质:旋转前后两图形全等,即对应线段相等,对应角相等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 在如图所示的网格中,每个小正方形边长为1.
在如图所示的网格中,每个小正方形边长为1.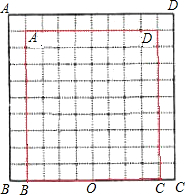 在如图所示的网格中,以BC的中点O为位似中心,把矩形ABCD缩小为原来的
在如图所示的网格中,以BC的中点O为位似中心,把矩形ABCD缩小为原来的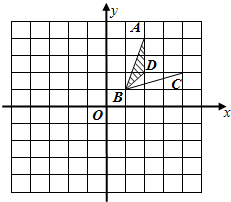 在如图所示的网格中,每个小方格的边长都是1.
在如图所示的网格中,每个小方格的边长都是1.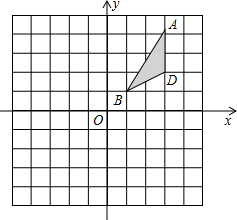 在如图所示的网格中,每个小方格的边长都是1.
在如图所示的网格中,每个小方格的边长都是1.