题目内容
如图9-2，△ABC中，∠B=90°,AB=6 cm，BC=8 cm，点P从点A开始沿AB边向B以
1 cm/s的速度移动，点Q从B点开始沿BC边向点C以2 cm/s的速度移动，①如果P、Q分别从A、B同时出发，经几秒钟，使△PBQ的面积等于8 cm2？②如果P、Q分别从A
、B同时出发，并且P到B后又继续在BC边上前进，Q到C后又继续在CA边上前进，经过几秒钟，使△PCQ的面积等于12.6 cm2？
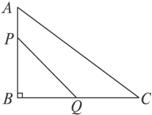
答案：①设x秒时，点P在
AB上，点Q在BC上，面积为8，
（6-x）·2x=8，解得x1=2，x2=4.
②设x秒时，点P移动到BC上，设点Q到BC的距离为h,则sinC=
=
.
由题意得（14-x）·
=12.6，
解得x1=7,x2=11.
当x=11秒时QC=14，Q点已超出CA的范围，故此解不合题意应舍去，所以经过7秒.
提示：设经过x秒，则AP=x，BQ=2x
，
∴BP=6-x.∴（6-x）·2x=8.
练习册系列答案
名校课堂系列答案
相关题目
25、如图，在锐角△ABC中，AB＞AC，AD⊥BC于D，以AD为直径的⊙O分别交AB，AC于E，F，连接DE，DF．
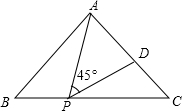如图，等腰直角△ABC的直角边长为3，P为斜边BC上一点，且BP=1，D为AC上一点，若∠APD=45°，则CD的长为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在Rt△ABC中，∠C=90°，AB=10cm，D为AB的中点，则CD=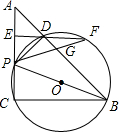
已知：如图，在Rt△ABC中，∠C=90°，AC=BC=4，P是AC上一动点（P不与A、C两点重合），连接PB，以PB为直径的圆交AB于点D，过点D作AC的垂线分别交AC于点E、交圆于点F，连接PF交AB于G．