题目内容
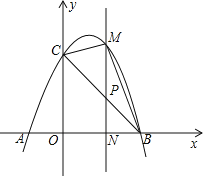
【题目】如图，已知抛物线
与
轴交于
、
两点（点在点的左边），与
轴交于点
，连接
.
（1）求、、三点的坐标；
（2）若点
为线段上的一点（不与、重合），
轴，且
交抛物线于点
，交轴于点
，当
的面积最大时，求
的周长.
【答案】（1）点
，
，
的坐标是：
；（2）
的周长
【解析】
（1）依据抛物线的解析式直接求得C的坐标，令y=0解方程即可求得A、B点的坐标；
（2）设
的面积为
，点
的坐标为
，则可表示出NM与BN，根据题意，
列式求解得
，则当
时，有最大值，则可求解的周长.
（1）由抛物线的解析式y=-x2+2x+3，
当
时，
，
∴C（0，3），
当
时，
，
解得：
，
，
，
点，，的坐标是：，
（2）设的面积为，点的坐标为，
则有
，
，
，
，
.
根据题意，
，
当时，有最大值，
此时，
，
，
，
.
，
根据勾股定理，得
，
的周长
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
