Question

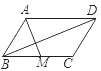
【题目】如图（1），在平行四边形ABCD中，AB=20， AD=30，∠ABC=60° ，点P从点D出发沿DC向点C匀速运动，速度为每秒3个单位长度； 同时，点Q从点B出发沿BA向点A匀速运动，速度为每秒2个单位长度.当点P停止运动时，点Q也随之停止运动. 过点P作PM⊥AD交AD于点M ，连接PQ，QM ，设运动的时间为t秒（）.

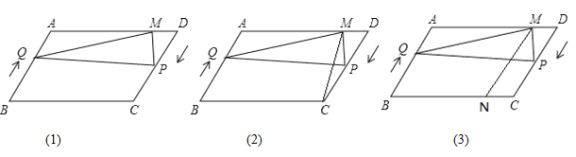
（1）当QP⊥PM时，求t的值；

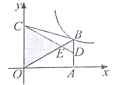
（2）如图（2）连接MC，是否存在t值 ，使得△PQM的面积是平行四边形ABCD面积的？ 若存在，求出对应的t值；若不存在， 请说明理由；

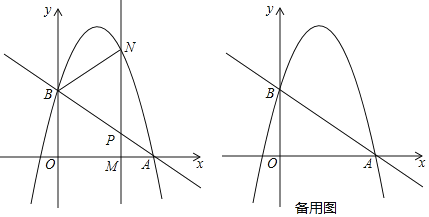
（3）如图（3），过点M作MN//AB交于点N，是否 存在t的值， 使得点P在线段MN的垂直平分线上？ 若存在， 求出对应的t的值；若不存在，请说明理由.

Answer 1

【答案】（1）t=4；（2）t＝6；（3）t=.

【解析】

（1）证明四边形AQPD是平行四边形，得AQ＝PD，然后列方程即可解决问题．

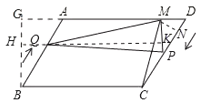
（2）作BG⊥DA交DA的延长线于G，过点Q作QK⊥PM于K，交BG于H，求出QK，PM，构建二次函数，然后过A作AI⊥BC于I，求出AI，得到平行四边形ABCD的面积，再利用面积关系建立方程即可得出结论；

（3）根据平行四边形的性质和等腰三角形的判定和性质证明NC＝PC，求出NC＝PC＝DM＝，再根据PC＋DP＝CD列出方程即可解决问题．

解：（1）∵PM⊥AD，QP⊥PM，

∴PQ∥AD，

∵四边形ABCD是平行四边形，

∴AB∥CD，

∴四边形AQPD是平行四边形，

∴AQ＝PD，

∴202t＝3t，

∴t＝4；

（2）如图，作BG⊥DA交DA的延长线于G，过点Q作QK⊥PM于K，交BG于H，则四边形GHKM是矩形，

在Rt△ABG中，∵∠G＝90°，∠ABG＝30°，AB＝20，

∴AG＝AB＝10，

在Rt△BHQ中，∵∠BHQ＝90°，∠HBQ＝30°，BQ＝2t，

∴HQ＝BQ＝t，

在Rt△PMD中，∵∠PMD＝90°，∠DPM＝30°，DP＝3t，

∴MD＝DP＝t，PM＝，

∴QK＝40tt＝，

∴S△QPM＝PMQK＝××（）＝，

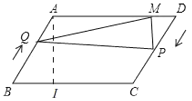
过A作AI⊥BC于I，

在Rt△ABI中，AI＝ABsin60°＝20×，

∴S四边形ABCD＝BCAI＝30×，

∵△PQM的面积是ABCD面积的，

∴，整理得：t216t＋60＝0，

解得：t＝6或t＝10（舍去），

即t＝6时，△PQM的面积是ABCD面积的；

（3）连接PN，

∵点P在线段MN的垂直平分线上，

∴PM＝PN，

∴∠PMN＝∠PNM，

∵AB∥MN，AM∥BN，

∴四边形ABNM是平行四边形，

∴∠AMN＝∠MNC＝∠B＝60°，

∵∠PMD＝90°，∠NMD＝120°，

∴∠PMN＝∠PNM＝∠PNC＝30°，

∵∠C＝120°，

∴∠CPN＝30°＝∠PNC，

∴NC＝PC＝DM＝，

∵PC＋DP＝20，

∴，

∴t＝，

即当t＝时，点P在线段MN的垂直平分线上．