题目内容
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数
y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.解答下面的问题:
(1)求过点P(1,4)且与已知直线y=-2x-1平行的直线l的函数表达式,并在图中画出直线l的图象;
(2)设直线l分别与y轴、x轴交于点A,B,如果直线m:y=kx+t(t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
答案:
解析:
解析:
|
解: (1)设直线l的表达式为y=-2x+b,把点P(1,4)代入,得4=-2+b,b=6,故直线l的函数表达式为y=-2x+6,图象如图所示;
(2)由x=0,得y=-2x+6=6,故A(0,6),由y=-2x+6=0,得x=3,故B(3,0). 因为直线 m:y=kx+t(t>0)与直线l:y=-2x+6平行,所以k=-2,且t≠6,由 x=0,得y=kx+t=t,故C(0,t),所以 AC=|6-t|,OB=3,所以S=当 0<t<6时,S=-当 t>6时,S= |

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目

 双曲线
双曲线 我们就称直线l1与直线l2互相平行.解答下面的问题:
我们就称直线l1与直线l2互相平行.解答下面的问题: 阅读下面的材料:
阅读下面的材料: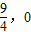 ),与双曲线
),与双曲线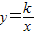 (x>0)交于点B.
(x>0)交于点B.

 :y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
:y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.