题目内容
 已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB,AC相交于D点,双曲线y=
已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB,AC相交于D点,双曲线y=| k |
| x |
①菱形OABC的面积为80;②E点的坐标是(4,8);③双曲线的解析式为y=
| 20 |
| x |
| 4 |
| 5 |
其中正确的结论有( )个.
分析:作DH⊥x轴于H,BG⊥x轴于G,根据菱形的面积等于对角线乘积的一半得到菱形OABC的面积=
OB•AC=
×160=80;则△ODA的面积为20,根据三角形面积公式可计算出DA=4,再根据菱形的性质易得DH为△OBG的中位线,则BG=8,所以E点的纵坐标为8;接着证明Rt△DOH∽Rt△ADH,得到DH2=OH•AH,
由于DH=4,AH=10-OH,则OH(10-OH)=16,解得OH=8或OH=2(舍去),可确定D点坐标为(8,4),利用待定系数法得到反比例函数解析式为y=
;同时可确定E点坐标为(4,8);CM⊥x轴于M,则CM=8,根据菱形性质得OC=OA=10,根据勾股定理可计算出OM=6,然后利用正弦的定义即可得到sin∠COM=
=
,于是有sin∠COA=
.
| 1 |
| 2 |
| 1 |
| 2 |
由于DH=4,AH=10-OH,则OH(10-OH)=16,解得OH=8或OH=2(舍去),可确定D点坐标为(8,4),利用待定系数法得到反比例函数解析式为y=
| 32 |
| x |
| CM |
| OC |
| 4 |
| 5 |
| 4 |
| 5 |
解答:解: 作DH⊥x轴于H,BG⊥x轴于G,如图,
作DH⊥x轴于H,BG⊥x轴于G,如图,
∵四边形OABC为菱形,
∴菱形OABC的面积=
OB•AC=
×160=80,所以①正确;
∴
DH•OA=菱形OABC的面积的
=
×80,
而A点的坐标为(10,0),
∴
DH×10=
×80,
∴DH=4,
∵OB与AC互相垂直平分,
∴∠AOD=90°,DH为△OBG的中位线,
∴BG=2DH=8,
∴E点的纵坐标为8,
∵∠DOH+∠ODH=∠ODH+∠ADH=90°,
∴∠DOH=∠ADH,
∴Rt△DOH∽Rt△ADH,
∴DH:AH=OH:DH,即DH2=OH•AH,
∵DH=4,AH=OA-OH=10-OH,
∴OH(10-OH)=16,解得OH=8或OH=2(舍去),
∴D点坐标为(8,4),
把D(8,4)代入y=
得k=4×8=32,
∴反比例函数解析式为y=
,所以③错误;
把y=8代入得
=8,解得x=4,
∴E点坐标为(4,8),所以②正确;
CM⊥x轴于M,如图,
∴CM=BG=8,
∵四边形OABC为菱形,
∴OC=OA=10,
在Rt△OCM中,CM=8,OC=10,
∴OM=
=6,
∴sin∠COM=
=
=
,
即sin∠COA=
,所以④正确.
故选C.
 作DH⊥x轴于H,BG⊥x轴于G,如图,
作DH⊥x轴于H,BG⊥x轴于G,如图,∵四边形OABC为菱形,
∴菱形OABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
而A点的坐标为(10,0),
∴
| 1 |
| 2 |
| 1 |
| 4 |
∴DH=4,
∵OB与AC互相垂直平分,
∴∠AOD=90°,DH为△OBG的中位线,
∴BG=2DH=8,
∴E点的纵坐标为8,
∵∠DOH+∠ODH=∠ODH+∠ADH=90°,
∴∠DOH=∠ADH,
∴Rt△DOH∽Rt△ADH,
∴DH:AH=OH:DH,即DH2=OH•AH,
∵DH=4,AH=OA-OH=10-OH,
∴OH(10-OH)=16,解得OH=8或OH=2(舍去),
∴D点坐标为(8,4),
把D(8,4)代入y=
| k |
| x |
∴反比例函数解析式为y=
| 32 |
| x |
把y=8代入得
| 32 |
| x |
∴E点坐标为(4,8),所以②正确;
CM⊥x轴于M,如图,
∴CM=BG=8,
∵四边形OABC为菱形,
∴OC=OA=10,
在Rt△OCM中,CM=8,OC=10,
∴OM=
| OC2-CM2 |
∴sin∠COM=
| CM |
| OC |
| 8 |
| 10 |
| 4 |
| 5 |
即sin∠COA=
| 4 |
| 5 |
故选C.
点评:本题考查了反比例函数的综合题:反比例函数图象的点的坐标满足其函数解析式;熟练运用菱形的性质、相似三角形的相似比和勾股定理进行计算.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目

 的图象的一个分支位于第一象限.
的图象的一个分支位于第一象限.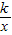 的图象的图象上,求k的值;
的图象的图象上,求k的值; S1?
S1?
 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
