题目内容
小尧和小淇手上分别有一个箱子,每个箱子里面各有两个球,小尧的箱子放入一黑一白,小淇的箱子放入两颗白球.由小尧的箱子任取一球放到小淇的箱子,再由小淇的箱子任取一球放回小尧的箱子,这样的流程称为“一轮”,一轮后拿到黑球者赢,则一轮过后小尧赢的概率是 .
考点:列表法与树状图法
专题:
分析:由小尧的箱子任取一球放到小淇的箱子,取得黑球与白球的概率均为:
,再由小淇的箱子任取一球放回小尧的箱子,取得黑球的概率为:
×
,继而求得答案.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
解答:解:∵小尧的箱子任取一球放到小淇的箱子,取得黑球与白球的概率均为:
,
再由小淇的箱子任取一球放回小尧的箱子,取得黑球的概率为:
×
,
∴一轮过后小尧赢的概率是:
+
×
=
.
故答案为:
.
| 1 |
| 2 |
再由小淇的箱子任取一球放回小尧的箱子,取得黑球的概率为:
| 1 |
| 3 |
| 1 |
| 2 |
∴一轮过后小尧赢的概率是:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:此题考查概率的求法.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
相关题目
以下计算正确的是( )
| A、3a2•4ab=7a3b |
| B、(2ab3)•(-4ab)=-2a2b4 |
| C、(xy)3•(-x2y)=-x3y3 |
| D、-3a2b(-3ab)=9a3b2 |
若x2=4,|y|=1,且x>y,则x+y的值为( )
| A、5 | B、±3 |
| C、3或1 | D、-3或-1 |
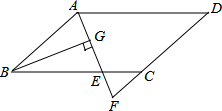 如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=4,则△CEF的面积是( )
如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=4,则△CEF的面积是( ) 如图,在3×3的幻方的九个空格中,填入9个数字,使得处于同一横行、同一竖行、同一斜对角线上的三个数的和都相等.下图是小兰同学要填的幻方,其中有三格被涂黑了,请你根据幻方的填数规则,求出x的值.
如图,在3×3的幻方的九个空格中,填入9个数字,使得处于同一横行、同一竖行、同一斜对角线上的三个数的和都相等.下图是小兰同学要填的幻方,其中有三格被涂黑了,请你根据幻方的填数规则,求出x的值.