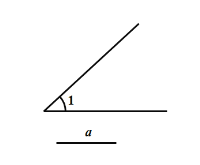题目内容
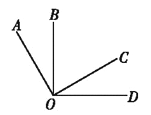
【题目】如图1,![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,
,![]() ,将一直角三角板(
,将一直角三角板(![]() )的直角顶点放在点
)的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 与
与![]() 都在直线
都在直线![]() 的上方.
的上方.
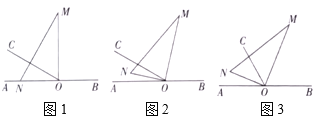
(1)将图1中的三角板绕点![]() 以每秒
以每秒![]() 的速度沿顺时针方向旋转一周.如图2,经过
的速度沿顺时针方向旋转一周.如图2,经过![]() 秒后,边
秒后,边![]() 恰好平分
恰好平分![]() .求
.求![]() 的值;
的值;
(2)在(1)问条件的基础上,若三角板在转动的同时,射线![]() 也绕
也绕![]() 点以每秒
点以每秒![]() 的速度沿顺时针方向旋转一周,如图3,那么经过多长时间
的速度沿顺时针方向旋转一周,如图3,那么经过多长时间![]() 平分
平分![]() ?请说明理由;
?请说明理由;
【答案】(1)5秒;(2)5秒时OC平分∠MON,理由见解析
【解析】
(1)由OM平分∠BOC,得∠COM=∠MOB,结合∠AOC=30°,得∠COM=75°,进而得∠AON=15°,即可得到答案;
(2)由三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,得∠AON=3t,∠AOC=30°+6t,由OC平分∠MON,得∠CON=∠COM=45°,进而列出关于t的方程,即可求解.
(1)∵∠AON+∠MON+∠BOM=180°,∠MON=90°,
∴∠AON+∠BOM=90°,
∵OM平分∠BOC,
∴∠COM=∠MOB,
∵∠AOC=30°,
∴∠BOC=2∠COM=150°,
∴∠COM=75°,
∴∠CON=15°,
∴∠AON=∠AOC-∠CON=30°-15°=15°,
∴t=15÷3=5秒;
(2)经过5秒时,OC平分∠MON,理由如下:
∵∠AON+∠BOM=90°,∠CON=∠COM,
∵∠MON=90°,
∴∠CON=∠COM=45°,
∵三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,
∴∠AON=3t,∠AOC=30°+6t,
∵∠AOC-∠AON=45°,
∴30°+6t-3t=45°,
解得:t=5秒;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目