Question

【题目】在中，点在边上，联结.

如图，将沿着翻折，点的对应点是点，若平分，则的值等于 ；

若.将绕着点旋转，使得点的对应点落在边上，点的对应点分别是点，则的面积等于 .

Answer 1

【答案】(1)120;(2)3或9.

【解析】

（1）根据翻折的性质和邻补角的性质列方程求解即可；

（2）分别按顺时针和逆时针旋转90°两种情画出图形，根据旋转的性质求解即可.

解：（1）∵将沿着翻折，点的对应点是点，

∴=,

∵平分，

∴∠ADB= =n°.

∵∠ADB+∠ADC=180°,

∴n°+ n°=180°

解之得,n=120.

故答案为120.

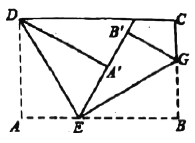
(2)①当△ABC绕点D顺时针旋转90°时,如图所示:

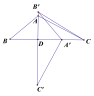
∵是由绕着点顺时针旋转90°得到,

∴ , ,

∵CD=4,

∴ =4-2=2.

∴的面积= =3;

②当△ABC绕点D逆时针旋转90°时,如图所示:

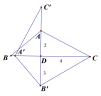
∵是由绕着点顺时针旋转90°得到,

∴ , ,

∴.

∴的面积= =9.

综上所述, 的面积等于3或9.

故答案为3或9.