题目内容
 如图,PM=PN,MQ为△PMN的角平分线.若∠MQN=72°,则∠P的度数是
如图,PM=PN,MQ为△PMN的角平分线.若∠MQN=72°,则∠P的度数是
- A.18°
- B.36°
- C.48°
- D.60°
B
分析:设∠P=x°,根据等腰三角形的性质和三角形的内角和为180°,可知∠PMN=(90- x)°,再根据角平分线的定义可得∠PMQ=
x)°,再根据角平分线的定义可得∠PMQ= (90-
(90- x)°,根据三角形外角的性质可得关于x的方程,可求出解.
x)°,根据三角形外角的性质可得关于x的方程,可求出解.
解答:设∠P=x°,则∠PMN= (180°-x)=(90-
(180°-x)=(90- x)°,
x)°,
∵MQ为△PMN的角平分线,
∴∠PMQ= (90-
(90- x)°,
x)°,
∴ (90-
(90- x)+x=72,
x)+x=72,
解得x=36.
故选:B.
点评:本题考查三角形外角的性质,等腰三角形的性质:两个底角相等,以及三角形的内角和为180°.
分析:设∠P=x°,根据等腰三角形的性质和三角形的内角和为180°,可知∠PMN=(90-
 x)°,再根据角平分线的定义可得∠PMQ=
x)°,再根据角平分线的定义可得∠PMQ= (90-
(90- x)°,根据三角形外角的性质可得关于x的方程,可求出解.
x)°,根据三角形外角的性质可得关于x的方程,可求出解.解答:设∠P=x°,则∠PMN=
 (180°-x)=(90-
(180°-x)=(90- x)°,
x)°,∵MQ为△PMN的角平分线,
∴∠PMQ=
 (90-
(90- x)°,
x)°,∴
 (90-
(90- x)+x=72,
x)+x=72,解得x=36.
故选:B.
点评:本题考查三角形外角的性质,等腰三角形的性质:两个底角相等,以及三角形的内角和为180°.

练习册系列答案
相关题目
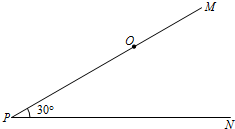 如图,PM,PN是两条夹角为30°的笔直的公路,在距离点P为8千米的点O处,有一个小灵通信号发射中心,在它的周围5千米(包括5千米)范围内小灵通才可以正常使用.小王早上8:00钟从点P出发,乘坐速度为每小时30千米的汽车向PN方向行进,若小王身上带的通讯工具只有小灵通,现要打电话给小王,问在什么时刻开始拨打为好?通话时间最多可以是几分钟?(结果精确到分)
如图,PM,PN是两条夹角为30°的笔直的公路,在距离点P为8千米的点O处,有一个小灵通信号发射中心,在它的周围5千米(包括5千米)范围内小灵通才可以正常使用.小王早上8:00钟从点P出发,乘坐速度为每小时30千米的汽车向PN方向行进,若小王身上带的通讯工具只有小灵通,现要打电话给小王,问在什么时刻开始拨打为好?通话时间最多可以是几分钟?(结果精确到分)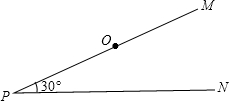 如图,PM,PN是两条夹角为30°的笔直的公路,在距离点P为8千米的点O处,有一个小灵通信号发射中心,在它的周围5千米(包括5千米)范围内小灵通才可以正常使用.小王早上8:00钟从点P出发,乘坐速度为每小时30千米的汽车向PN方向行进.
如图,PM,PN是两条夹角为30°的笔直的公路,在距离点P为8千米的点O处,有一个小灵通信号发射中心,在它的周围5千米(包括5千米)范围内小灵通才可以正常使用.小王早上8:00钟从点P出发,乘坐速度为每小时30千米的汽车向PN方向行进. 如图,PM是垂线,PN是水平线,PM与PN相交于点P,圆心在水平线PN上的⊙O半径为1cm,圆心O到垂线PM的距离OP=3cm.若垂线PM向右平移,当PM与⊙O相切时,垂线PM平移的距离为
如图,PM是垂线,PN是水平线,PM与PN相交于点P,圆心在水平线PN上的⊙O半径为1cm,圆心O到垂线PM的距离OP=3cm.若垂线PM向右平移,当PM与⊙O相切时,垂线PM平移的距离为 如图,PM⊥OA于M,PN⊥OB于N,PM=PN,∠BOC=30°,则∠AOB=
如图,PM⊥OA于M,PN⊥OB于N,PM=PN,∠BOC=30°,则∠AOB=