题目内容
含30°角的直角三角板ABC中,∠A=30°.将其绕直角顶点C顺时针旋转 角(
角( 且
且 ≠ 90°),得到Rt△
≠ 90°),得到Rt△ ,
, 边与AB所在直线交于点D,过点 D作DE∥
边与AB所在直线交于点D,过点 D作DE∥ 交
交 边于点E,连接BE.
边于点E,连接BE.
(1)如图1,当 边经过点B时,
边经过点B时, = °;
= °;
(2)在三角板旋转的过程中,若∠CBD的度数是∠CBE度数的m倍,猜想m的值并证明你的结论;
(3) 设 BC=1,AD=x,△BDE的面积为S,以点E为圆心,EB为半径作⊙E,当S=
时,求AD的长,并判断此时直线 与⊙E的位置关系.
与⊙E的位置关系.
(1)60
(2)证明略
(3)直线 与⊙E相交
与⊙E相交
解析

练习册系列答案
相关题目
 14、把两个一样大的含30°角的直角三角板按如图的方式拼在一起,其中AC平分∠BAF,AD平分∠EAF,请写出所有的等腰三角形:
14、把两个一样大的含30°角的直角三角板按如图的方式拼在一起,其中AC平分∠BAF,AD平分∠EAF,请写出所有的等腰三角形: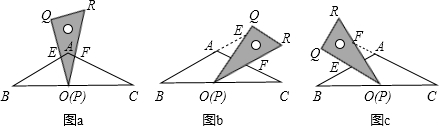
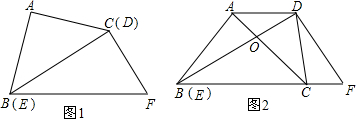

 如图,有一位同学用一个含30°角的直角三角板估测学校的旗杆AB的高度,他将30°角的直角边水平放在1.3米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为15米,则旗杆AB的高度为( )(
如图,有一位同学用一个含30°角的直角三角板估测学校的旗杆AB的高度,他将30°角的直角边水平放在1.3米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为15米,则旗杆AB的高度为( )(