题目内容
?ABCD的对角线相交于点O，点E、F在BD上，且BE=DF，四边形AECF是平行四边形吗？为什么？
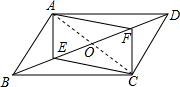解：四边形AECF是平行四边形．理由：
连接AC交BD于点O
∵平行四边形ABCD
∴AO=CO，BO=DO
∵BE=DF
∴BO-BE=DO-DF
∴EO=FO
∴四边形AECF是平行四边形．
分析：可连接AO，证四边形AECF的对角线互相平分即可．
点评：此题主要考查了平行四边形的判定和性质：平行四边形的对角线互相平分；对角线互相平分的四边形是平行四边形．
练习册系列答案
相关题目
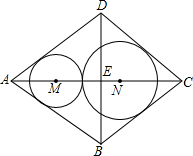形零件（菱形铁片上只能加工同一直径的零件，不计加工过程中的损耗），问加工哪种零件能最充分地利用这种铁片并说明理由．
如图，已知矩形ABCD的对角线AC，BD的相交点O，E、F、G、H分别是OA、OB、OC、OD的中点．平行四边形ABCD的对角线AC和BD相交点O，与△OBC面积相等的三角形（不包括自身）的个数是
| A． 1 | B．2 | C．3 | D．4 |
如图，已知矩形ABCD的对角线AC，BD的相交点O，E、F、G、H分别是OA、OB、OC、OD的中点．