题目内容
若函数y=4x2-4ax+a2+1(0≤x≤2)的最小值为3,求a的值.
解:∵y=4x2-4ax+a2+1(0≤x≤2),
∴y=4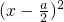 +1,
+1,
(1)当0≤ ≤2,即0≤a≤4时,最小值为1,不符合题意,舍去;
≤2,即0≤a≤4时,最小值为1,不符合题意,舍去;
(2)当 <0即a<0时,令f(0)=3得:a2+1=3,解得:a=±
<0即a<0时,令f(0)=3得:a2+1=3,解得:a=± ,故a=-
,故a=- ;
;
(3)当 >2即a>4时,令f(2)=3,即a2-8a+14=0,解得;a=4±
>2即a>4时,令f(2)=3,即a2-8a+14=0,解得;a=4± ,故a=4+
,故a=4+ ;
;
综上有;a=- 或4+
或4+ .
.
分析:把函数y=4x2-4ax+a2+1(0≤x≤2)化为y=4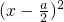 +1,分类讨论
+1,分类讨论 的大小即可得出答案.
的大小即可得出答案.
点评:本题考查了二次函数的最值,难度不大,关键是用分类讨论的思想进行解题.
∴y=4
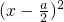 +1,
+1,(1)当0≤
 ≤2,即0≤a≤4时,最小值为1,不符合题意,舍去;
≤2,即0≤a≤4时,最小值为1,不符合题意,舍去;(2)当
 <0即a<0时,令f(0)=3得:a2+1=3,解得:a=±
<0即a<0时,令f(0)=3得:a2+1=3,解得:a=± ,故a=-
,故a=- ;
;(3)当
 >2即a>4时,令f(2)=3,即a2-8a+14=0,解得;a=4±
>2即a>4时,令f(2)=3,即a2-8a+14=0,解得;a=4± ,故a=4+
,故a=4+ ;
;综上有;a=-
 或4+
或4+ .
.分析:把函数y=4x2-4ax+a2+1(0≤x≤2)化为y=4
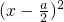 +1,分类讨论
+1,分类讨论 的大小即可得出答案.
的大小即可得出答案.点评:本题考查了二次函数的最值,难度不大,关键是用分类讨论的思想进行解题.

练习册系列答案
相关题目
若函数y=4x2+1的函数值为5,则自变量x的值应为( )
| A、1 | ||||
| B、-1 | ||||
| C、±1 | ||||
D、
|


