Question

【题目】

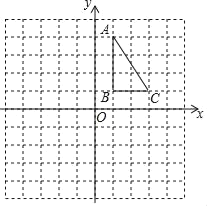
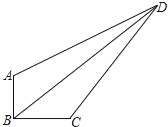
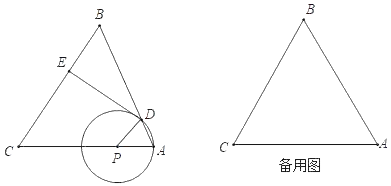
如图，△ABC中，AC＝BC＝10，cosC＝，点P是AC边上一动点（不与点A、C重合），以PA长为半径的⊙P与边AB的另一个交点为D，过点D作DE⊥CB于点E．

（1）当⊙P与边BC相切时，求⊙P的半径．

（2）连接BP交DE于点F，设AP的长为x，PF的长为y，求y关于x的函数解析式，并直接写出x的取值范围．

（3）在（2）的条件下，当以PE长为直径的⊙Q与⊙P相交于AC边上的点G时，求相交所得的公共弦的长.

Answer 1

【答案】（1）;（2）;（3）.

【解析】

（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝，则sinC＝，sinC＝＝＝，即可求解；

（2）首先证明PD∥BE，则，即：，即可求解；

（3）证明四边形PDBE为平行四边形，则AG＝EP＝BD，即：AB＝DB+AD＝AG+AD＝4，即可求解．

（1）设⊙P与边BC相切的切点为H，圆的半径为R，

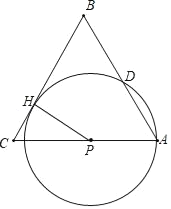
连接HP，则HP⊥BC，cosC＝，则sinC＝，

sinC＝＝＝，解得：R＝；

（2）在△ABC中，AC＝BC＝10，cosC＝，

设AP＝PD＝x，∠A＝∠ABC＝β，过点B作BH⊥AC，

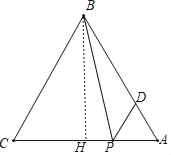
则BH＝ACsinC＝8，

同理可得：CH＝6，HA＝4，AB＝4，则：tan∠CAB＝2，

BP＝＝，

DA＝x，则BD＝4﹣x，

如下图所示，PA＝PD，∴∠PAD＝∠CAB＝∠CBA＝β，

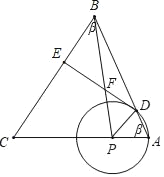
tanβ＝2，则cosβ＝，sinβ＝，

EB＝BDcosβ＝（4﹣x）×＝4﹣x，

∴PD∥BE，

∴，即：，

整理得：y＝；

（3）以EP为直径作圆Q如下图所示，

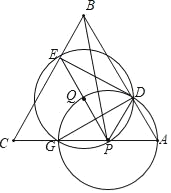
两个圆交于点G，则PG＝PQ，即两个圆的半径相等，则两圆另外一个交点为D，

GD为相交所得的公共弦，

∵点Q是弧GD的中点，

∴DG⊥EP，

∵AG是圆P的直径，

∴∠GDA＝90°，

∴EP∥BD，

由（2）知，PD∥BC，∴四边形PDBE为平行四边形，

∴AG＝EP＝BD，

∴AB＝DB+AD＝AG+AD＝4，

设圆的半径为r，在△ADG中，

AD＝2rcosβ＝，DG＝，AG＝2r，

+2r＝4，解得：2r＝，

则：DG＝＝50﹣10，

相交所得的公共弦的长为50﹣10．