题目内容
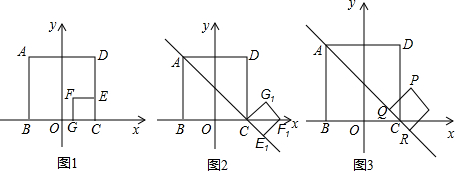
图1是两个正方形纸片ABCD和CEFG叠放在一起,分别以BC边所在直线和BC边的中垂线为坐标轴建立如图所示的坐标系,其中B(﹣2,0),E(2,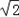 ),C(2,0),固定正方形ABCD,直线L经过AC两点;将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1.
),C(2,0),固定正方形ABCD,直线L经过AC两点;将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1.
(1)在图2中求点E1的坐标,并直接写出点E1与直线L的位置关系.
(2)利用(1)的结论,将图2中的正方形CE1F1G1在射线CA上沿着CA方向以每秒1个单位的速度平移,平移后的正方形CE1F1G1设为正方形PQRH(图3),当点R移动到点A停止,设正方形PQRH移动的时间为t秒,正方形PQRH与正方形ABCD重叠部分的面积为S,请直接写出S与t之间的函数解析式,并写出函数自变量t的取值范围.
(3)在(2)的条件下,如果S=1时,过BP的直线为m,M点为直线m上的动点,N为直线L上的动点,那么是否存在平行四边形MNBC,如果存在,请求出M点的坐标,如果不存在,请说明理由.
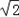 ),C(2,0),固定正方形ABCD,直线L经过AC两点;将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1.
),C(2,0),固定正方形ABCD,直线L经过AC两点;将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1.(1)在图2中求点E1的坐标,并直接写出点E1与直线L的位置关系.
(2)利用(1)的结论,将图2中的正方形CE1F1G1在射线CA上沿着CA方向以每秒1个单位的速度平移,平移后的正方形CE1F1G1设为正方形PQRH(图3),当点R移动到点A停止,设正方形PQRH移动的时间为t秒,正方形PQRH与正方形ABCD重叠部分的面积为S,请直接写出S与t之间的函数解析式,并写出函数自变量t的取值范围.
(3)在(2)的条件下,如果S=1时,过BP的直线为m,M点为直线m上的动点,N为直线L上的动点,那么是否存在平行四边形MNBC,如果存在,请求出M点的坐标,如果不存在,请说明理由.

解:(1)由E点坐标可知正方形CEFG边长为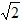 ,
,
那么其对角线CF长度为2,
正方形CEFG绕点C顺时针旋转135° 后,
CE与x轴夹角为45°,
C坐标为(2,0),
那么E1坐标为(3,﹣1),E1在直线L上;
(2)当0≤t≤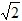 时,S=
时,S=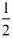 t2;
t2;
当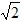 <t≤2
<t≤2 时,S=﹣
时,S=﹣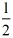 t2+2
t2+2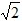 t﹣2;
t﹣2;
当2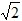 <t≤3
<t≤3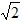 时,S=2;
时,S=2;
当3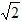 <t≤4
<t≤4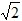 时 S=﹣
时 S=﹣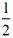 t2+3
t2+3 t﹣7;
t﹣7;
当4 <t≤5
<t≤5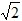 时,S=
时,S=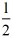 t2﹣5
t2﹣5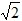 t+25;
t+25;
(3)S=1时,当t≤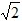 时,
时,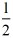 t2=1,解得:t=
t2=1,解得:t= ;
;
当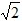 <t≤2
<t≤2 时,2﹣
时,2﹣ (2
(2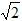 ﹣t)2=1,解得:t=
﹣t)2=1,解得:t=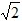 或3
或3 (舍去);
(舍去);
当2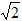 <t≤4
<t≤4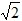 时,
时, (4
(4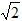 ﹣t)2=1,解得:t=3
﹣t)2=1,解得:t=3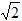 或5
或5 (5
(5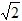 不合题意,舍去).
不合题意,舍去).
则t=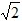 或3
或3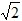 .
.
①当t=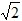 时,那么P位于CD中点处,P的坐标是:(2,2),
时,那么P位于CD中点处,P的坐标是:(2,2),
设直线m的解析式是y=kx+b,
则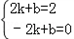 ,解得:
,解得: ,
,
则直线m表达式y=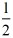 x+1,直线L表达式y=﹣x+2,
x+1,直线L表达式y=﹣x+2,
设MN的纵坐标是a,
则在y=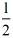 x+1中,令y=a,解得:x=2(a﹣1),
x+1中,令y=a,解得:x=2(a﹣1),
则M的横坐标是2(a﹣1);
在y=﹣x+2中,令y=a,则x=2﹣a,
即N的横坐标是:(2﹣a).
∵BC=4,
则:2(a﹣1)﹣(2﹣a)=4,解得:a= ,
,
把y= 代入y=
代入y=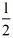 x+1中,解得:x=
x+1中,解得:x=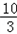 .
.
则M的坐标为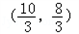 ;
;
②当t=3 时,P是AD与y轴的交点,则P的坐标是:(0,4).
时,P是AD与y轴的交点,则P的坐标是:(0,4).
设直线m的解析式是y=kx+b,
则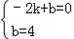 ,解得:
,解得: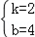 ,
,
则m的解析式是:y=2x+4.
同①方法相同,设MN的纵坐标是a,
则在y=2x+4中,令y=a,解得:x= (a﹣4),
(a﹣4),
则M的横坐标是 (a﹣1);
(a﹣1);
在y=﹣x+2中,令y=a,则x=2﹣a,
即N的横坐标是:(2﹣a).
根据BC=4,则: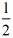 (a﹣4)﹣(2﹣a)=4,
(a﹣4)﹣(2﹣a)=4,
解得:a=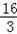 ,把y=
,把y=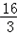 代入y=2x+4中,解得x=
代入y=2x+4中,解得x= .
.
则M的坐标是:( ,
,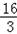 ).
).
故M的坐标是:( ,
, )或(
)或( ,
, ).
).
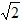 ,
,那么其对角线CF长度为2,
正方形CEFG绕点C顺时针旋转135° 后,
CE与x轴夹角为45°,
C坐标为(2,0),
那么E1坐标为(3,﹣1),E1在直线L上;
(2)当0≤t≤
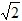 时,S=
时,S=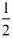 t2;
t2;当
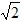 <t≤2
<t≤2 时,S=﹣
时,S=﹣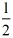 t2+2
t2+2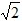 t﹣2;
t﹣2;当2
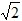 <t≤3
<t≤3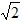 时,S=2;
时,S=2;当3
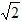 <t≤4
<t≤4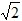 时 S=﹣
时 S=﹣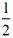 t2+3
t2+3 t﹣7;
t﹣7;当4
 <t≤5
<t≤5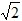 时,S=
时,S=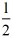 t2﹣5
t2﹣5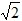 t+25;
t+25;(3)S=1时,当t≤
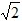 时,
时,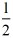 t2=1,解得:t=
t2=1,解得:t= ;
;当
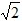 <t≤2
<t≤2 时,2﹣
时,2﹣ (2
(2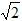 ﹣t)2=1,解得:t=
﹣t)2=1,解得:t=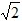 或3
或3 (舍去);
(舍去);当2
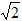 <t≤4
<t≤4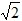 时,
时, (4
(4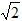 ﹣t)2=1,解得:t=3
﹣t)2=1,解得:t=3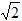 或5
或5 (5
(5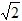 不合题意,舍去).
不合题意,舍去).则t=
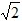 或3
或3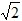 .
.①当t=
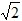 时,那么P位于CD中点处,P的坐标是:(2,2),
时,那么P位于CD中点处,P的坐标是:(2,2),设直线m的解析式是y=kx+b,
则
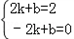 ,解得:
,解得: ,
,则直线m表达式y=
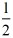 x+1,直线L表达式y=﹣x+2,
x+1,直线L表达式y=﹣x+2,设MN的纵坐标是a,
则在y=
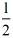 x+1中,令y=a,解得:x=2(a﹣1),
x+1中,令y=a,解得:x=2(a﹣1),则M的横坐标是2(a﹣1);
在y=﹣x+2中,令y=a,则x=2﹣a,
即N的横坐标是:(2﹣a).
∵BC=4,
则:2(a﹣1)﹣(2﹣a)=4,解得:a=
 ,
,把y=
 代入y=
代入y=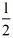 x+1中,解得:x=
x+1中,解得:x=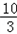 .
.则M的坐标为
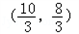 ;
;②当t=3
 时,P是AD与y轴的交点,则P的坐标是:(0,4).
时,P是AD与y轴的交点,则P的坐标是:(0,4).设直线m的解析式是y=kx+b,
则
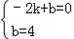 ,解得:
,解得: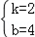 ,
,则m的解析式是:y=2x+4.
同①方法相同,设MN的纵坐标是a,
则在y=2x+4中,令y=a,解得:x=
 (a﹣4),
(a﹣4),则M的横坐标是
 (a﹣1);
(a﹣1);在y=﹣x+2中,令y=a,则x=2﹣a,
即N的横坐标是:(2﹣a).
根据BC=4,则:
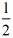 (a﹣4)﹣(2﹣a)=4,
(a﹣4)﹣(2﹣a)=4,解得:a=
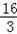 ,把y=
,把y=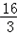 代入y=2x+4中,解得x=
代入y=2x+4中,解得x= .
.则M的坐标是:(
 ,
,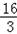 ).
).故M的坐标是:(
 ,
, )或(
)或( ,
, ).
).
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
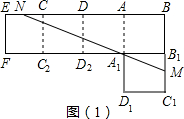
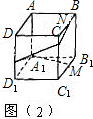

 ,则乙正方形的面积是多少平方厘米?
,则乙正方形的面积是多少平方厘米?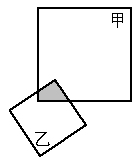
 ),C(2,0),固定正方形ABCD,直线L经过AC两点;将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1,
),C(2,0),固定正方形ABCD,直线L经过AC两点;将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1,