Question

【题目】阅读下列两则材料，回答问题

材料一：我们将+与﹣称为一对“对偶式”因为（+）（）＝（）2＝a﹣b，所以构造“对偶式”相乘可以将+与﹣中的“”去掉．

例如：已知＝2，求+的值，

解：（）（+）＝（25﹣x）﹣（15﹣x）＝10，

∵﹣＝2，

∴+＝5，

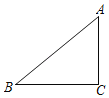
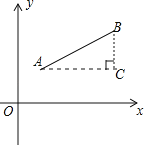
材料二：如图1，点A（x1，y1），点B（x2，y2），以AB为斜边作Rt△ABC，则C（x2，y1）AC＝|x1﹣x2|，BC＝|y1﹣y2|．所以AB＝．反之，可将代数式的值看作点A（x1，y1）到点B（x2，y2）的距离，例如＝＝＝，所以可将代数式的值看作点（x，y）到点（1，﹣1）的距离．

（1）利用材料一，解关于x的方程：＝5，其中x≤10；

（2）利用材料二，求代数式+ 的最小值，并求出此时y与x的函数关系式，写出x的取值范围；

（3）在（2）的条件下，设该式子取得最小值时的图形端点为M、N，直接写出将y与x的函数图象向左平移_____个单位时恰好经过点Q（﹣2，），并直接判定此时△MNQ的形状是______三角形．

Answer 1

【答案】（1）x＝9；（2）y＝﹣7x+11（1≤x≤2）；最小值为5；（3），锐角．

【解析】

（1）根据（+）（﹣）＝25﹣x﹣10+x＝15，+＝5，推出﹣＝3，求出，的值即可解决问题．

（2）由代数式＝，可知求代数式的最小值，可以转化为找一点P（x，y），使得点P到M（1，4）和N（2，﹣3）的距离之和最小，这个最小值是线段MN的长，点P在线段MN上，由此即可解决问题．

（3）设平移后的直线的解析式为y＝﹣7x+m，把点Q（﹣2，）代入，可得平移后的直线的解析式为y＝﹣7x﹣，求出两直线与x轴的交点坐标，即可求出平移的距离，再利用两点间距离公式，结合勾股定理的逆定理即可解决问题．

解：（1）∵（+）（﹣）＝25﹣x﹣10+x＝15， +＝5，

∴﹣＝3，

∴＝4，＝1，

∴x＝9．

（2）∵代数式+

＝+，

∴求代数式+的最小值，可以转化为找一点P（x，y），使得点P到M（1，4）和N（2，﹣3）的距离之和最小，这个最小值是线段MN的长，点P在线段MN上，

∵MN＝＝5，

∴代数式+的最小值为5，

设直线MN的解析式为y＝kx+b，则有，

解得，

∴此时y与x的函数关系式：y＝﹣7x+11（1≤x≤2）．

（3）设平移后的直线的解析式为y＝﹣7x+m，

把点Q（﹣2，）代入得到：＝14+m，

m＝﹣，

∴平移后的直线的解析式为y＝﹣7x﹣，

∵直线y＝﹣7x+11交x轴于（，0），直线y＝﹣7x﹣交x轴于（﹣，0），

∴平移的距离＝+＝，

∵M（1，4），N（2，﹣3），Q（﹣2，），

∴MN2＝50，MQ2＝32+（）2，NQ2＝42+（）2，

∴MN＞MQ，MN＞NQ，

∵MQ2+NQ2＝25+＜50，

∴∠MQN＜90°，

∴△MNQ是锐角三角形．

故答案为，锐角．