题目内容
正方形ABCD的边长为3,E,F 分别是AB,BC边上的点,且∠EDF=45°.将
△DAE绕点D逆时针旋转90°,得到△DCM.

(1)求证:EF=FM;
(2)当AE=1时,求EF的长.
【答案】
(1)见解析 (2)
【解析】(1)证明:∵△DAE逆时针旋转90°得到△DCM,∴∠FCM=∠FCD+∠DCM=180°,
∴ F,C,M三点共线,DE=DM,∠EDM=90°,∴∠EDF+∠FDM=90°.
∵ ∠EDF=45°,∴∠FDM=∠EDF=45°.
在△DEF和△DMF中,DE=DM,∠EDF=∠MDF,DF=DF,
∴△DEF≌△DMF(SAS),∴ EF=MF.
(2)解:设EF=MF=x,∵AE=CM=1,且BC=3,∴ BM=BC+CM=3+1=4,
∴BF=BM-MF=BM-EF=4-x.
∵EB=AB-AE=3-1=2,在Rt△EBF中,
由勾股定理得EB2+BF2=EF2,即22+(4-x)2=x2,
解得:x= ,即EF=
,即EF= .
.

练习册系列答案
相关题目
 附加题
附加题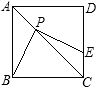 如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3
如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3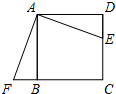 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为 如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=
如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=