题目内容
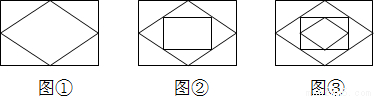
顺次连接矩形各边的中点所得的四边形是
- A.矩形
- B.菱形
- C.正方形
- D.不能确定
B
分析：根据三角形的中位线定理和菱形的判定，顺次连接矩形各边中点所得的四边形是菱形．
解答：
解：如图：E，F，G，H为矩形的中点，则AH=HD=BF=CF，AE=BE=CG=DG，
在Rt△AEH与Rt△DGH中，AH=HD，AE=DG，
∴△AEH≌△DGH，
∴EH=HG，
同理，△AEH≌△DGH≌△BEF≌△CGF≌△DGH
∴EH=HE=GF=EF，∠EHG=∠EFG，
∴四边形EFGH为菱形．
故选：B．
点评：此题主要考查了菱形的判定，综合利用了三角形的中位线定理和矩形的性质是解题关键．
分析：根据三角形的中位线定理和菱形的判定，顺次连接矩形各边中点所得的四边形是菱形．
解答：
解：如图：E，F，G，H为矩形的中点，则AH=HD=BF=CF，AE=BE=CG=DG，在Rt△AEH与Rt△DGH中，AH=HD，AE=DG，
∴△AEH≌△DGH，
∴EH=HG，
同理，△AEH≌△DGH≌△BEF≌△CGF≌△DGH
∴EH=HE=GF=EF，∠EHG=∠EFG，
∴四边形EFGH为菱形．
故选：B．
点评：此题主要考查了菱形的判定，综合利用了三角形的中位线定理和矩形的性质是解题关键．
练习册系列答案
相关题目
