题目内容
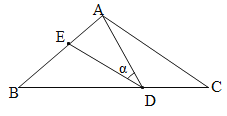
【题目】如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=![]() .有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或
.有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或![]() ;④0<BE≤
;④0<BE≤![]() ,其中正确的结论是 (填入正确结论的序号).
,其中正确的结论是 (填入正确结论的序号).
【答案】②③.
【解析】
试题分析:∵∠ADE=∠B=∠α,∠EAD=∠EAD,∴△ADE∽△ABD,而△ABD不一定相似△ACD,故①不正确;
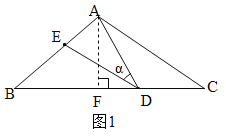
过A作AF⊥BC于F,如图1,∵AB=AC,∴BF=FC,∵tan∠α=![]() ,∠B=∠α,∴tanB=
,∠B=∠α,∴tanB=![]() ,∴cosB=
,∴cosB=![]() ,∴
,∴![]() ,∴BF=
,∴BF=![]() AB=12,∴BC=24,∵DC=9,∴BD=BC-DC=15,∴BD=AC,∵AB=AC,∴∠B=∠C,∴∠α=∠C,∵∠C+∠CAD=∠α+∠BDE,∴∠BDE=∠CAD,在△BED和△CDA中,∵∠BDE=∠CAD,BD=AC,∠B=∠C,∴△BDE≌△CAD,故②正确;
AB=12,∴BC=24,∵DC=9,∴BD=BC-DC=15,∴BD=AC,∵AB=AC,∴∠B=∠C,∴∠α=∠C,∵∠C+∠CAD=∠α+∠BDE,∴∠BDE=∠CAD,在△BED和△CDA中,∵∠BDE=∠CAD,BD=AC,∠B=∠C,∴△BDE≌△CAD,故②正确;
若△BDE为直角三角形,则有两种情况:(1)若∠BED=90°,∵∠BDE=∠CAD,∠B=∠C,∴△BDE∽△CAD,∴∠CDA=∠BED=90°,∴AD⊥BC,∵AB=AC,∴BD=![]() BC=12;
BC=12;
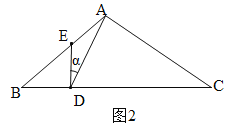
(2)若∠BDE=90°,如图2,设BD=x,则DC=24-x,∵∠CAD=∠BDE=90°,∠B=∠C=∠α,∴cos∠C=cosB=![]() ,∴
,∴![]() ,解得:
,解得:![]() ,∴若△BDE为直角三角形,则BD为12或
,∴若△BDE为直角三角形,则BD为12或![]() ,故③正确;
,故③正确;
设BE=x,CD=y,∵△BDE∽△CAD,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴0<BE≤
,∴0<BE≤![]() ,∴故④错误;
,∴故④错误;
故答案为:②③.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目