题目内容
如图,⊙O是等腰三角形ABC的外接圆,AB=AC,∠A=45°,BD为⊙O的直径,BD与AC相交于点E ,
,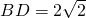 ,连接CD.
,连接CD.
(1)试求BC的长及圆心O到弦BC的距离;
(2)求出∠AEB的度数.
 解:(1)过点O作OF⊥BC于点F
解:(1)过点O作OF⊥BC于点F∵BD为⊙O的直径
∴BC⊥DC
∵∠A=∠BDC=45°
∴△BCD为等腰直角三角形
∵BD=

∴BC=CD=
 ×
× =2,OF=
=2,OF= CD=1
CD=1∴BC=2,圆心O到弦BC的距离为1;
(2)∵∠A=45°,AB=AC
∴∠ACB=
 (180°-45°)=67.5°
(180°-45°)=67.5°∵∠DBC=45°
∴∠AEB=∠DBC+∠ACB=112.5°
∴∠AEB=112.5°.
分析:(1)作辅助线,过点O作OF⊥BC于点F,由BD是⊙O的直径,可知BC⊥DC,由圆周角定理得∠A=∠BDC=45°,故△ACD为等腰直角三角形,已知BD=
 ,可求CD=BC=2,OF=
,可求CD=BC=2,OF= CD;
CD;(2)已知∠A的度数,AB=AC,可求出∠ACB的值,由(1)知∠DBC的值,代入∠AEB=∠DBC+∠ACB,进行求解即可.
点评:本题主要考查圆周角定理的应用,关键是知△BCD为等腰直角三角形.

练习册系列答案
相关题目


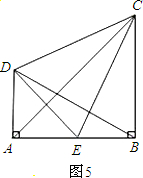
 7、如图,在三角测平架中,AB=AC.在BC的中点D处挂一重锤,让它自然下垂.如果调整架身,使重锤线正好经过点A,那么就能确认BC处于水平位置.这是为什么?
7、如图,在三角测平架中,AB=AC.在BC的中点D处挂一重锤,让它自然下垂.如果调整架身,使重锤线正好经过点A,那么就能确认BC处于水平位置.这是为什么?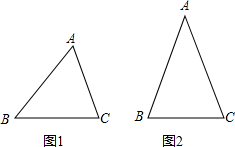 小华同学学习了第二十五章《锐角三角比》后,对求三角形的面积方法进行了研究,得到了新的结论:
小华同学学习了第二十五章《锐角三角比》后,对求三角形的面积方法进行了研究,得到了新的结论: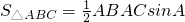 ;
;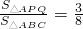 ?
?
 有下面4个结论:
有下面4个结论: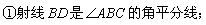 ②
②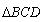 是等腰三角
是等腰三角
