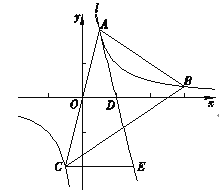
题目内容
【题目】如图, ![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() 延长线上任意一点,以
延长线上任意一点,以![]() 为直角边作等腰直角
为直角边作等腰直角![]() ,且
,且![]() ,连结
,连结![]() .
.
(![]() )求证:
)求证: ![]() .
.
(![]() )在点
)在点![]() 运动过程中,试问
运动过程中,试问![]() 的度数是否会变化?若不变,请求出它的度数,若变化,请说明它的变化趋势.
的度数是否会变化?若不变,请求出它的度数,若变化,请说明它的变化趋势.
(![]() )已知
)已知![]() ,设
,设![]() ,
, ![]() .
.
①试求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
②当![]() 时,求
时,求![]() 的外接圆半径.
的外接圆半径.

【答案】(![]() )见解析;(
)见解析;(![]() )结论:
)结论: ![]() 的度数是定值,
的度数是定值, ![]() ;(
;(![]() )①
)①![]() ,
,
②![]() 的外接圆的半径为
的外接圆的半径为![]() .
.
【解析】试题分析: ![]() 设
设![]() 与
与![]() 交于点
交于点![]() ,由
,由![]() ,推出
,推出![]() ,,推出
,,推出![]() ,
, ![]() ,推出
,推出![]() ,
,
推出![]() ,由
,由![]() ,推出
,推出![]() ,即可解决问题.
,即可解决问题.
(2)结论: ![]() 的度数是定值,
的度数是定值, ![]() .由(1)可知△
.由(1)可知△![]() ,即可推出
,即可推出![]()
(3)①在![]() 中,由
中,由![]() ,推出BC=AC=1,在
,推出BC=AC=1,在![]() 中,
中, ![]() ,由
,由![]() ,推出
,推出![]() ,推出
,推出![]() ,可得
,可得![]() ,根据
,根据![]() 计算即可.②取
计算即可.②取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,
,
由![]() 推出
推出![]() 推出点
推出点![]() 是
是![]() 的外接圆的圆心,求出线段
的外接圆的圆心,求出线段![]() 即可解决问题.
即可解决问题.
试题解析:(![]() )证明:如图,设
)证明:如图,设![]() 与
与![]() 交于点
交于点![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
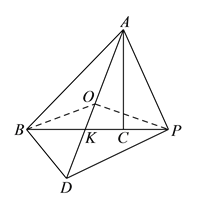
(![]() )结论:
)结论: ![]() 的度数是定值,
的度数是定值, ![]() .
.
理由:由(![]() )可知
)可知![]() ,
,
∴![]() ,
,
∴点![]() 运动过程中,
运动过程中, ![]() 的度数是定值,
的度数是定值,
![]() .
.
(![]() )①在
)①在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
![]() .
.
②取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴点![]() 是
是![]() 的外接圆的圆心,
的外接圆的圆心,
∵![]() ,
,
∴![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
∴![]() ,
,
由(![]() )可知
)可知![]() ,
,
∴![]() ,
,
在![]() 中,
中,
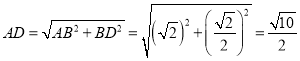 ,
,
∴![]() .
.
∴![]() 的外接圆的半径为
的外接圆的半径为![]() .
.

练习册系列答案
相关题目