题目内容
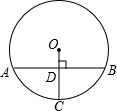（2012•瑶海区一模）如图半径为13的⊙O中，弦AB垂直于半径OC交OC于D，AB=24，则CD的长为（ ）分析：连接OA，先根据垂径定理求出AD的长，再根据勾股定理求出OD的长，根据CD=OC-OD即可得出结论．
解答：
解：连接OA，
∵AB⊥OC，AB=24，
∴AD=
AB=
×24=12，
在Rt△AOD中，
∵OA=13，AD=12，
∴OD=
=
=5，
∴CD=OC-OD=13-5=8．
故选C．
解：连接OA，∵AB⊥OC，AB=24，
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOD中，
∵OA=13，AD=12，
∴OD=
| OA2-AD2 |
| 132-122 |
∴CD=OC-OD=13-5=8．
故选C．
点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形，利用勾股定理求解是解答此题的关键．
练习册系列答案
相关题目
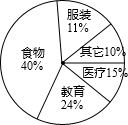（2012•瑶海区一模）在春节期间，小明对自己家7天的家庭开支情况进行了统计，各类支出如图所示，用于食物费用为800元，那么本月用于教育的费用为（ ）
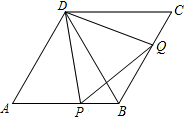（2012•瑶海区一模）在菱形ABCD中，∠A=60°，点P、Q分别在边AB、BC上，且AP=BQ．试判断△PDQ的形状，并证明．
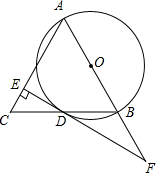（2012•瑶海区一模）如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC于点E，交AB的延长线于点F．