题目内容
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径.点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.
(1)通过角度的转化和逆运算求证(2)6
解析试题分析:、(1)证明:连接OC, ……… 1分
∵点C在⊙O上,OA=OC,∴∠OCA=∠OAC. ……… 1分
∵CD⊥PA,∴∠CDA=90°,
∴∠CAD+∠DCA=90°.
∵AC平分∠PAE,
∴∠DAC=∠CAO.
∴∠DCO=∠DCA+∠ACO=∠DCA+∠CAO=∠DCA+∠DAC=90°. ……… 1分
又∵点C在⊙O上,OC为⊙O的半径,
∴CD为⊙O的切线. ……… 1分
(2)解:过O作OF⊥AB,垂足为F, ……… 1分
∴∠OCD=∠CDA=∠OFD=90°,
∴四边形OCDF为矩形,
∴OC=FD,OF=CD.
∵DC+DA=6,设AD=x,则OF=CD=6-x.
∵⊙O的直径为10,∴DF=OC=5,
∴AF=5-x. ……… 1分
在Rt△AOF中,由勾股定理得
AF2+OF2=OA2.
即(5-x)2+(6-x)2=25,
化简得:x2-11x+18=0,
解得x=2或x=9.
由AD<DF,知0<x<5,故x=2. ……… 1分
∴AD=2, AF=5-2=3.
∵OF⊥AB,由垂径定理知,F为AB的中点,
∴AB=2AF=6.
考点:二次函数的综合题
点评:在解题时要能灵运用二次函数的图象和性质求出二次函数的解析式,利用数形结合思想解题是本题的关键

练习册系列答案
相关题目
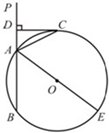 23、如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD丄PA,垂足为D.
23、如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD丄PA,垂足为D.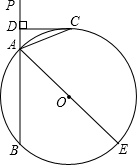 (2012•昌平区一模)如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,C为⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA于D.
(2012•昌平区一模)如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,C为⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA于D. 如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
