题目内容
 你能利用右图证勾股定理吗?
你能利用右图证勾股定理吗?分析:根据梯形的面积等于三个直角三角形的面积之和列式整理即可得证.
解答:证明:图形的面积=
×(a+b)×(a+b)=
ab+
ab+
c2,
所以,a2+2ab+b2=2ab+c2,
所以,a2+b2=c2.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以,a2+2ab+b2=2ab+c2,
所以,a2+b2=c2.
点评:本题考查了勾股定理的证明,是基础题,利用图形的面积的两种表示方法列出等式是解题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
 如图所示,在边长为c的正方形中,有四个斜边为c、直角边为a,b的全等直角三角形,你能利用这个图说明勾股定理吗?写出理由.
如图所示,在边长为c的正方形中,有四个斜边为c、直角边为a,b的全等直角三角形,你能利用这个图说明勾股定理吗?写出理由. 的正方形中,有四个斜边为
的正方形中,有四个斜边为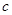 ,直角边为
,直角边为 的全等直角三角形,你能利用这个图说明勾股定理吗?写出理由。
的全等直角三角形,你能利用这个图说明勾股定理吗?写出理由。
 如图所示,在边长为c的正方形中,有四个斜边为c、直角边为a,b的全等直角三角形,你能利用这个图说明勾股定理吗?写出理由.
如图所示,在边长为c的正方形中,有四个斜边为c、直角边为a,b的全等直角三角形,你能利用这个图说明勾股定理吗?写出理由. 你能利用右图证勾股定理吗?
你能利用右图证勾股定理吗?