Question

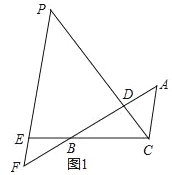
【题目】如图，在数轴．上有两个长方形和，这两个长方形的宽都是个单位长度，长方形的长是个单位长度，长方形的长是个单位长度，点在数轴上表示的数是，且两点之间的距离为．

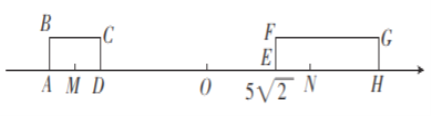
点在数轴上表示的数是 ，点在数轴上表示的数是

若线段的中点为，线段上有一点以每秒个单位长度的速度向右匀速运动，以每秒个单位长度的速度向左运动，设运动的时间为秒，问当为多少时，原点恰为线段的三等分点?

若线段的中点为，线段上有一点，长方形以每秒个单位长度的速度向右匀速运动，长方形保持不动，设运动时间为秒，是否存在一个的值，使以三点为顶点的三角形是直角三角形?若存在，求的值;不存在，请说明理由．

Answer 1

【答案】（1）；（2）或；（3）存在这样的t，t的值为或．

【解析】

（1）根据已知条件得出点H在点E右边个单位处，点A在点E左边个单位处，再根据点E表示的数即可得出答案；

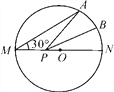
（2）根据条件算出点M、点N表示的数，然后再分OM=2ON和ON=2OM两种情况，根据条件列出含有绝对值的方程求解即可；

（3）分、和三种情况讨论，根据条件建立方程求解即可．

解：（1）∵点在数轴上表示的数是，，

∴，即点H在数轴上表示的数是，

∵，，

∴，

∴，即点A在数轴上表示的数是；

（2）由题意知，线段的中点为，则表示的数为，线段上有一点，且，则表示的数为，

∵以每秒个单位长度的速度向右匀速运动，以每秒个单位长度的速度向左运动，

∴经过秒后，点表示的数为，点表示的数为，

①当时，则有，

解得（经检验，不符合题意，舍去）或，

②当时，则有，

解得（经检验，不符合题意，舍去），

综上所述，当或时，原点恰为线段的三等分点；

（3）根据题意，因为点的位置不确定，所以应分类讨论，有以下三种情况：

①当时，点与点重合，此时；

②当时，，

由题可得，，

，

，

，

，

解得；

③，

综上所述，存在这样的t，t的值为或．