题目内容
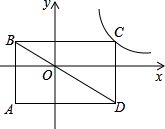（2013•新民市一模）如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y=| k2+2k+1 | x |
1或-3
1或-3
．分析：根据矩形的对角线将矩形分成面积相等的两个直角三角形，找到图中的所有矩形及相等的三角形，即可推出S四边形CEOF=S四边形HAGO，根据反比例函数比例系数的几何意义即可求出k2+4k+1=4，再解出k的值即可．
解答：解：如图：
∵四边形ABCD、HBEO、OECF、GOFD为矩形，
又∵BO为四边形HBEO的对角线，OD为四边形OGDF的对角线，
∴S△BEO=S△BHO，S△OFD=S△OGD，S△CBD=S△ADB，
∴S△CBD-S△BEO-S△OFD=S△ADB-S△BHO-S△OGD，
∴S四边形HAGO=S四边形CEOF=2×2=4，
∴xy=k2+2k+1=4，
解得k=1或k=-3．
故选D．
∵四边形ABCD、HBEO、OECF、GOFD为矩形，
又∵BO为四边形HBEO的对角线，OD为四边形OGDF的对角线，
∴S△BEO=S△BHO，S△OFD=S△OGD，S△CBD=S△ADB，
∴S△CBD-S△BEO-S△OFD=S△ADB-S△BHO-S△OGD，
∴S四边形HAGO=S四边形CEOF=2×2=4，
∴xy=k2+2k+1=4，
解得k=1或k=-3．
故选D．
点评：本题考查了反比例函数k的几何意义、矩形的性质、一元二次方程的解法，关键是判断出S四边形CEOF=S四边形HAGO．
练习册系列答案
相关题目
（2013•新民市一模）如图是由五个相同的小立方块搭成的几何体，这个几何体的主视图是（ ）