题目内容
如图正方形ABCD的顶点C在直线a上，且点B，D到a的距离分别是1，2．则这个正方形的边长为
- A.1
- B.2
- C.4
- D.
D
分析：先证明△BMC≌△NCD，再用勾股定理即可求解．
解答：∵∠MBC+∠BCM=∠NCD+∠BCM=90°
∴∠MBC=∠NCD
又∠BMC=∠CND=90°，BC=CD
∴△BMC≌△NCD
∴MC=ND=2
∴BC=
=
故选D．
点评：本题考查直角三角形全等的判定和勾股定理的应用．
分析：先证明△BMC≌△NCD，再用勾股定理即可求解．
解答：∵∠MBC+∠BCM=∠NCD+∠BCM=90°
∴∠MBC=∠NCD
又∠BMC=∠CND=90°，BC=CD
∴△BMC≌△NCD
∴MC=ND=2
∴BC=
=故选D．
点评：本题考查直角三角形全等的判定和勾股定理的应用．
练习册系列答案
相关题目
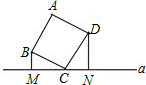如图正方形ABCD的顶点C在直线a上，且点B，D到a的距离分别是1，2．则这个正方形的边长为（ ）| A、1 | ||
| B、2 | ||
| C、4 | ||
D、
|
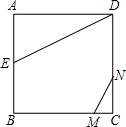如图正方形ABCD的边长为2，AE=EB，线段MN的两端点分别在CB、CD上滑动，且MN=1，当CM为何值时△AED与以M、N、C为顶点的三角形相似？
如图正方形ABCD的边BC的延长线上取点M，使CM=AC=2，AM与CD相交于点N，∠ANC=
（2013•鄂州）如图正方形ABCD的边长为4，E、F分别为DC、BC中点．
如图正方形ABCD的边长是a，△AEF是等边三角形，点E在BC上，点F在CD上