题目内容
已知：△ABC中，D，E分别是AB，AC的中点，S△ABC=16cm2，则S△ADE=
- A.16cm2
- B.12cm2
- C.8cm2
- D.4cm2
D
分析：由中位线定理可得线段DE与BC的比，即可得出△ADE与△ABC的比，又已知△ABC的面积，进而即可得出△ADE的面积．
解答：
解：如图，
∵D，E分别是AB，AC的中点，
∴DE：BC=1：2，
∴
=
，
又∵S△ABC=16，
∴S△ADE=4．
故选D．
点评：本题主要考查了三角形的中位线定理以及相似三角形面积比与对应边之比的关系，能够熟练掌握．
分析：由中位线定理可得线段DE与BC的比，即可得出△ADE与△ABC的比，又已知△ABC的面积，进而即可得出△ADE的面积．
解答：
解：如图，∵D，E分别是AB，AC的中点，
∴DE：BC=1：2，
∴
=，又∵S△ABC=16，
∴S△ADE=4．
故选D．
点评：本题主要考查了三角形的中位线定理以及相似三角形面积比与对应边之比的关系，能够熟练掌握．
练习册系列答案
阅读快车系列答案
相关题目
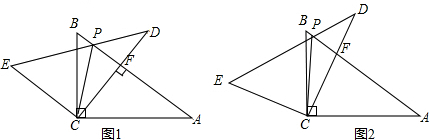
如图所示，已知在△ABC中，AB=AC，∠BAD=β，且AD=AE，求∠EDC．（用β表示）
8、如图，已知在△ABC中，AD垂直平分BC，AC=EC，点B、D、C、E在同一直线上，则下列结论：①AB=AC；②∠CAE=∠E；③AB+BD=DE；④∠BAC=∠ACB．正确的个数有（ ）个．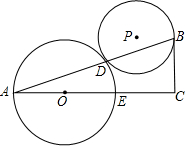
外切于点D，若AC和BC边的长是关于x的方程x2-（AB+4）x+4AB+8=0的两根，且25BC•sinA=9AB，