题目内容
如图4，将矩形ABCD绕点A顺时针旋转90o后，得到矩形AB’C’D’，若CD=8，AD=6，连接CC’，那么CC’的长是
A．20
B．10
C．10
D．100
【答案】
B.
【解析】
试题分析：矩形ABCD绕点A顺时针旋转90°得到矩形AB′C′D′，可知旋转中心为点A，旋转角∠CAC′=90°，根据对应点C、C′到旋转中心的距离相等可知，AC=AC′，先在Rt△ACD中用勾股定理求AC，再在Rt△CAC′中，利用勾股定理求CC′．
由旋转的性质可知，∠CAC′=90°，AC=AC′，
Rt△ACD中，由勾股定理得，
AC=
，
在Rt△CAC′中，由勾股定理得，
CC′=
．
故选B.
考点: 旋转的性质．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
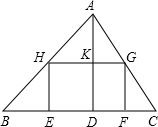如图所示，某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造．已知△ABC的边BC长120米，高AD长80米．学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分（如图）．其中矩形EFGH的一边EF在边BC上．其中两个顶点H、G分别在边AB、AC上．现计划在△AHG上种草，在△BHE、△GFC上都种花，在矩形EFGH上兴建喷泉．当FG长为多少米时，种草的面积与种花的面积相等？
时，求出y的值；
