题目内容
 如图,已知点C,D在线段AB上,M、N分别是AC、BD的中点,若AB=20,CD=4,
如图,已知点C,D在线段AB上,M、N分别是AC、BD的中点,若AB=20,CD=4,(1)求MN的长.
(2)若AB=a,CD=b,请用含有a、b的代数式表示出MN的长.
分析:(1)先根据线段和差的定义得出AC+DB=AB-CD=16,再由线段中点的定义,得MC=
AC,ND=
DB,则MC+DN=8,然后根据MN=MC+CD+ND即可求解;
(2)同(1),先根据线段和差的定义得出AC+DB=AB-CD=a-b,再由线段中点的定义,得MC=
AC,ND=
DB,则MC+DN=
(a-b),然后根据MN=MC+CD+ND即可求解.
| 1 |
| 2 |
| 1 |
| 2 |
(2)同(1),先根据线段和差的定义得出AC+DB=AB-CD=a-b,再由线段中点的定义,得MC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵AB=20,CD=4,
∴AC+DB=AB-CD=16.
∵M、N分别是AC、BD的中点,
∴MC=
AC,ND=
DB,
∴MC+DN=
AC+
DB=
(AC+DB)=8,
∴MN=MC+CD+DN
=(MC+DN)+CD
=8+4
=12;
(2)∵AB=a,CD=b,
∴AC+DB=AB-CD=a-b.
∵M、N分别是AC、BD的中点,
∴MC=
AC,ND=
DB,
∴MC+DN=
AC+
DB=
(AC+DB)=
(a-b),
∴MN=MC+CD+DN
=(MC+DN)+CD
=
(a-b)+b
=
.
∴AC+DB=AB-CD=16.
∵M、N分别是AC、BD的中点,
∴MC=
| 1 |
| 2 |
| 1 |
| 2 |
∴MC+DN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=MC+CD+DN
=(MC+DN)+CD
=8+4
=12;
(2)∵AB=a,CD=b,
∴AC+DB=AB-CD=a-b.
∵M、N分别是AC、BD的中点,
∴MC=
| 1 |
| 2 |
| 1 |
| 2 |
∴MC+DN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=MC+CD+DN
=(MC+DN)+CD
=
| 1 |
| 2 |
=
| a+b |
| 2 |
点评:此题考查了线段中点的定义及线段的和差计算,属于基础知识,本题由第一问到第二问的设计体现了由特殊到一般,由具体到抽象的思维过程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
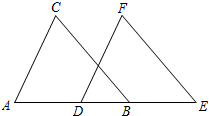 如图,已知点B、D在直线AE上,AC∥DF,∠C=∠F,AD=BE,试说明BC∥EF的理由.
如图,已知点B、D在直线AE上,AC∥DF,∠C=∠F,AD=BE,试说明BC∥EF的理由. BD于点E,BD=8,CM=2.
BD于点E,BD=8,CM=2. (2013•建邺区一模)如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.
(2013•建邺区一模)如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F. 如图,已知点A,B分别在x轴和y轴上,且OA=OB=
如图,已知点A,B分别在x轴和y轴上,且OA=OB= 如图,已知点D、F在线段BC上,点E在线段BA的延长线上,EF与AC交于点G,且∠EFC=∠ADC,∠AGE=∠E.请说出AD平分∠BAC的理由.
如图,已知点D、F在线段BC上,点E在线段BA的延长线上,EF与AC交于点G,且∠EFC=∠ADC,∠AGE=∠E.请说出AD平分∠BAC的理由.