题目内容
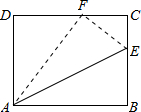 如图,长方形的长AB=10,宽BC=8,E在BC上,沿AE对折点B恰好落在DC上的F点,求DF、BE的长.
如图,长方形的长AB=10,宽BC=8,E在BC上,沿AE对折点B恰好落在DC上的F点,求DF、BE的长.分析:由折叠的性质可得AF=AB=10,在RT△ADF中可求出DF的长度,进而设BE=x,则EF=x,CE=8-x,CF=10-DF,利用勾股定理可得出BE的长度.
解答:解:由折叠的性质可得,AF=AB=10,
在RT△ADF中,DF=
=6;
设BE=x,则EF=x,CE=8-x,CF=10-DF=4,
在RT△EFC中,EF2=CE2+CF2,即x2=(8-x)2+42,
解得:x=3,即BE=3;
综上可得:DF=6,BE=3.
在RT△ADF中,DF=
| AF2-AD2 |
设BE=x,则EF=x,CE=8-x,CF=10-DF=4,
在RT△EFC中,EF2=CE2+CF2,即x2=(8-x)2+42,
解得:x=3,即BE=3;
综上可得:DF=6,BE=3.
点评:此题考查了翻折变换的知识,解答本题的关键是掌握翻折前后对应边相等,另外要熟练勾股定理在解直角三角形中的应用.

练习册系列答案
相关题目
 6、如图,长方形的长为a,宽为b,横向阴影部分为长方形,另一阴影部分为平形四边形,它们的宽都为c,则空白部分的面积是( )
6、如图,长方形的长为a,宽为b,横向阴影部分为长方形,另一阴影部分为平形四边形,它们的宽都为c,则空白部分的面积是( ) 17、如图,长方形的长为a,宽为b,横向阴影部分为长方形,另一阴影部分为平行四边形,它们的宽都为c,则空白部分的面积是
17、如图,长方形的长为a,宽为b,横向阴影部分为长方形,另一阴影部分为平行四边形,它们的宽都为c,则空白部分的面积是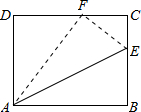 如图,长方形的长AB=10,宽BC=8,E在BC上,沿AE对折点B恰好落在DC上的F点,求DF、BE的长.
如图,长方形的长AB=10,宽BC=8,E在BC上,沿AE对折点B恰好落在DC上的F点,求DF、BE的长.