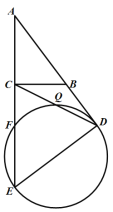
题目内容
【题目】一边长为4正方形![]() 放在平面直角坐标系中,其中
放在平面直角坐标系中,其中![]() 为原点,点
为原点,点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上,
轴上,![]() 为射线
为射线![]() 上任意一点
上任意一点
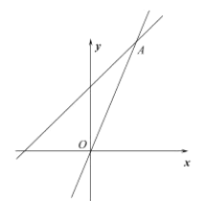
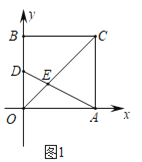
(1)如图1,若点![]() 坐标为
坐标为![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的面积为__________;
的面积为__________;
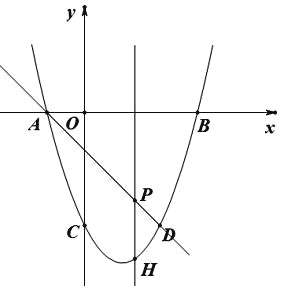
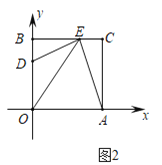
(2)如图2,将![]() 沿
沿![]() 翻折得
翻折得![]() ,若点
,若点![]() 在直线
在直线![]() 图象上,求出
图象上,求出![]() 点坐标;
点坐标;
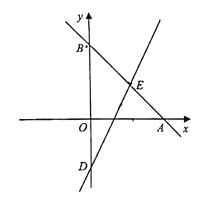
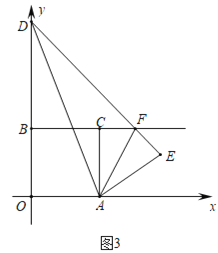
(3)如图3,将![]() 沿
沿![]() 翻折得
翻折得![]() ,
,![]() 和射线
和射线![]() 交于点
交于点![]() ,连接
,连接![]() ,若
,若![]() ,平面内是否存在点
,平面内是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角边的等腰直角三角形,若存在,请求出所有点
为直角边的等腰直角三角形,若存在,请求出所有点![]() 坐标:若不存在,请说明理由.
坐标:若不存在,请说明理由.
【答案】(1)![]() ;(2)E(
;(2)E(![]() ,
,![]() );(3)Q(
);(3)Q(![]() ,
,![]() ),Q'(
),Q'(![]() ,
,![]() ),Q'(0,
),Q'(0,![]() ),Q''(8,
),Q''(8,![]() )
)
【解析】
(1)由待定系数法可求直线OC,直线AD的解析式,再求出交点E的坐标,由三角形面积公式可求解;
(2)如图2,过点E作EH⊥OA,由折叠的性质可得AO=AE=4,设点E(a,![]() a),求出AH,再由勾股定理列方程求出a的值即可;
a),求出AH,再由勾股定理列方程求出a的值即可;
(3)由折叠的性质可得∠DAO=∠DAE=75°,OA=AE,∠DOA=∠DEA=90°,由“HL”可证Rt△AEF≌Rt△ACF,可得∠CAF=∠EAF=30°,然后求出CF=![]() ,再分两种情况讨论,由全等三角形的性质和等腰直角三角形的性质求解即可.
,再分两种情况讨论,由全等三角形的性质和等腰直角三角形的性质求解即可.
解:(1)∵边长为4的正方形OACB放在平面直角坐标系中,
∴点A(4,0),点C(4,4),点D(0,2),
∴直线OC解析式为:y=x,
设直线AD解析式为:y=kx+b,
则![]() ,解得:
,解得: ,
,
∴直线AD解析式为:y=![]() x+2,
x+2,
联立 ,解得:
,解得:![]() ,
,
∴点E坐标(![]() ,
,![]() ),
),
∴△AOE的面积=![]() ×4×
×4×![]() =
=![]() ,
,
故答案为:![]() ;
;
(2)如图2,过点E作EH⊥OA,

∵将△AOD沿AD翻折得△AED,
∴AO=AE=4,
设点E(a,![]() a),
a),
∴OH=a,EH=![]() a,
a,
∴AH=4a,
∵AE2=EH2+AH2,
∴16=![]() a2+(4a)2,
a2+(4a)2,
∴a=0(舍去)或a=![]() ,
,
∴点E(![]() ,
,![]() );
);
(3)∵将△AOD沿AD翻折得△AED,
∴∠DAO=∠DAE=75°,OA=AE,∠DOA=∠DEA=90°,
∴∠OAE=150°,AE=AC,∠ACF=∠AED=90°,
∴∠CAE=60°,
∵AE=AC,AF=AF,
∴Rt△AEF≌Rt△ACF(HL),
∴∠CAF=∠EAF=30°,
∴AF=2CF,
∴AF2=AC2+CF2,即4CF2=16+CF2,
∴CF=![]() (负值舍去),
(负值舍去),
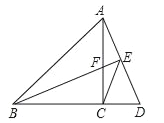
∵△AFQ是以AF为直角边的等腰直角三角形,
∴当∠AFQ=90°,AF=FQ时,如图3,过点Q作QN⊥BF于点N,
∴∠NQF+∠QFN=90°,且∠QFN+∠AFC=90°,
∴∠NQF=∠AFC,且∠ACF=∠QNF=90°,QF=AF,
∴△QNF≌△FCA(AAS),
∴QN=CF=![]() ,AC=NF=4,
,AC=NF=4,
∴Q(![]() ,
,![]() ),
),
同理可求:Q'(![]() ,
,![]() );
);
当∠FAQ=90°,AF=AQ时,
同理可求,Q'(0,![]() ),Q''(8,
),Q''(8,![]() ).
).