Question

如图，AB为⊙O的直径，AM和BN是它的两条切线，E为⊙O的半圆弧上一动点（不与A、B重合），过点E的直线分别交射线AM、BN于D、C两点，且CB＝CE．

 

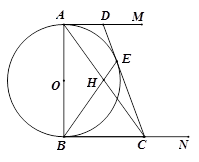
1.求证：CD为⊙O的切线

2.若tan∠BAC＝，求 的值

 

Answer 1

 

1.证明：连接OE．       …………………………………1分

∵OB＝OE，

∴∠OBE＝∠OEB．

∵BC＝EC，

∴∠CBE＝∠CEB．             ……………………………………………2分

∴∠OBC＝∠OEC．

∵BC为⊙O的切线，

∴∠OEC＝∠OBC＝90°，        ……………………………………………3分

∵OE为半径，∴CD为⊙O的切线．……………………………………………4分

2.延长BE交AM于点G，连接AE，过点D作DT⊥BC于点T．

因为DA、DC、CB为⊙O的切线，

∴DA＝DE，CB＝CE．

在Rt△ABC中，因为tan∠BAC＝，令AB＝2x，则BC＝x．

∴CE＝BC＝x．                ……………………………………………5分

令AD＝DE＝a，

则在Rt△DTC中，CT＝CB－AD＝x－a，DC＝CE＋DE＝x＋a，DT＝AB＝2x，

∵DT²＝DC²－CT²，

∴(2x)²＝(x＋a)²－(x－a)²．   ……………………………………………6分

解之得，x＝a．               ……………………………………………7分

∵AB为直径，

∴∠AEG＝90°．

∵AD＝ED，

∴AD＝ED＝DG＝a．

∴AG＝2a．                    ……………………………………………8分

因为AD、BC为⊙O的切线，AB为直径，

∴AG∥BC．

所以△AHG∽△CHB．

∴＝＝．        ……………………………………………9分

∴＝1．                 ……………………………………………10分

解析:切线的判定定理是圆中常考点，三角形相似是求三角形中线段长度的常用方法。