题目内容
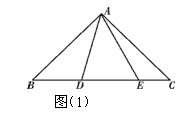
已知:如图(1)在Rt△ABC中,∠BAC=90°,AB = AC,点D、E分别为线段BC上两动点,若∠DAE=45°.探究线段BD、DE、EC三条线段之间的数量关系。 小明的思路是:把△AEC绕点A顺时针旋转90°,得到△ABE′,连结E'D,使问题得到解决。请你参考小明的思路探究并解决下列问题:
(1)猜想BD、DE、EC三条线段之间存在的数量关系式,并对你的猜想给予证明;
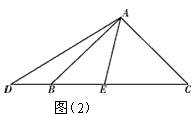
(2)当动点E在线段BC上,动点D运动在线段CB延长线上时,如图(2),其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明。
(1)猜想BD、DE、EC三条线段之间存在的数量关系式,并对你的猜想给予证明;
(2)当动点E在线段BC上,动点D运动在线段CB延长线上时,如图(2),其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明。
|

练习册系列答案
相关题目
 已知:如图,小明在打网球时,要使球恰好能打过网,而且落在离网5米的位置上,则球拍击球的高度h应为( )
已知:如图,小明在打网球时,要使球恰好能打过网,而且落在离网5米的位置上,则球拍击球的高度h应为( )| A、2.7m | B、1.8m | C、0.9m | D、6m |


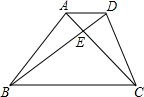 已知:如图所示,在梯形ABCD中,AD∥BC,对角线AC和BD相交于点E,且AC=AB,BD=BC,BA⊥AC于点A,求证:CD=CE.
已知:如图所示,在梯形ABCD中,AD∥BC,对角线AC和BD相交于点E,且AC=AB,BD=BC,BA⊥AC于点A,求证:CD=CE.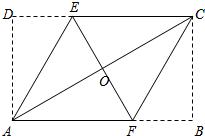 21、已知:如图所示,在矩形ABCD中,分别沿AE、CF折叠△ADE、△CBF,使得点D、点B都重合于点O,且E、O、F三点共线,A、O、C三点共线.
21、已知:如图所示,在矩形ABCD中,分别沿AE、CF折叠△ADE、△CBF,使得点D、点B都重合于点O,且E、O、F三点共线,A、O、C三点共线.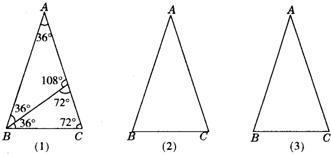
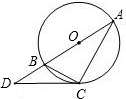 已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.
已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.