题目内容
【题目】如图,直线y=﹣ ![]() x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B两点.
x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B两点.
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的一点,连接PA、PB、PO,若△POA的面积是△POB面积的 ![]() 倍.
倍.
①求点P的坐标;
②点Q为抛物线对称轴上一点,请直接写出QP+QA的最小值;
(3)点M为直线AB上的动点,点N为抛物线上的动点,当以点O、B、M、N为顶点的四边形是平行四边形时,请直接写出点M的坐标.
【答案】
(1)解:∵直线y=﹣ ![]() x+1与x轴交于点A,与y轴交于点B,
x+1与x轴交于点A,与y轴交于点B,
∴A(2,0),B(0,1),
∵抛物线y=﹣x2+bx+c经过A、B两点,
∴ ![]() ,
,
∴ ![]()
∴抛物线解析式为y=﹣x2+ ![]() x+1
x+1
(2)解:①由(1)知,A(2,0),B(0,1),
∴OA=2,OB=1,
由(1)知,抛物线解析式为y=﹣x2+ ![]() x+1,
x+1,
∵点P是第一象限抛物线上的一点,
∴设P(a,﹣a2+ ![]() a+1),((a>0,﹣a2+
a+1),((a>0,﹣a2+ ![]() a+1>0),
a+1>0),
∴S△POA= ![]() OA×Py=
OA×Py= ![]() ×2×(﹣a2+
×2×(﹣a2+ ![]() a+1)=﹣a2+
a+1)=﹣a2+ ![]() a+1
a+1
S△POB= ![]() OB×Px=
OB×Px= ![]() ×1×a=
×1×a= ![]() a
a
∵△POA的面积是△POB面积的 ![]() 倍.
倍.
∴﹣a2+ ![]() a+1=
a+1= ![]() ×
× ![]() a,
a,
∴a= ![]() 或a=﹣
或a=﹣ ![]() (舍)
(舍)
∴P( ![]() ,1);
,1);
②如图1,
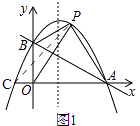
由(1)知,抛物线解析式为y=﹣x2+ ![]() x+1,
x+1,
∴抛物线的对称轴为x= ![]() ,抛物线与x轴的另一交点为C(﹣
,抛物线与x轴的另一交点为C(﹣ ![]() ,0),
,0),
∵点A与点C关于对称轴对称,
∴QP+QA的最小值就是PC= ![]()
(3)解:①当OB为平行四边形的边时,MN=OB=1,MN∥OB,
∵点N在直线AB上,
∴设M(m,﹣ ![]() m+1),
m+1),
∴N(m,﹣m2+ ![]() m+1),
m+1),
∴MN=|﹣m2+ ![]() m+1﹣(﹣
m+1﹣(﹣ ![]() m+1)|=|m2﹣2m|=1,
m+1)|=|m2﹣2m|=1,
Ⅰ、m2﹣2m=1,
解得,m=1± ![]() ,
,
∴M(1+ ![]() ,
, ![]() (1﹣
(1﹣ ![]() ))或M(1﹣
))或M(1﹣ ![]() ,
, ![]() (1+
(1+ ![]() ))
))
Ⅱ、m2﹣2m=﹣1,
解得,m=1,
∴M(1, ![]() );
);
②当OB为对角线时,OB与MN互相平分,交点为H,
∴OH=BH,MH=NH,
∵B(0,1),O(0,0),
∴H(0, ![]() ),
),
设M(n,﹣ ![]() n+1),N(d,﹣d2+
n+1),N(d,﹣d2+ ![]() d+1)
d+1)
∴ 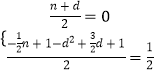 ,
,
∴ ![]() 或
或 ![]() ,
,
∴M(﹣(1+ ![]() ),
), ![]() (3+
(3+ ![]() ))或M(﹣(1﹣
))或M(﹣(1﹣ ![]() ),
), ![]() (3﹣
(3﹣ ![]() ));
));
即:满足条件的点M的坐标(1+ ![]() ,
, ![]() (1﹣
(1﹣ ![]() ))或(1﹣
))或(1﹣ ![]() ,﹣
,﹣ ![]() (1+
(1+ ![]() ))或(1,
))或(1, ![]() )或M(﹣(1+
)或M(﹣(1+ ![]() ),
), ![]() (3+
(3+ ![]() ))或M(﹣(1﹣
))或M(﹣(1﹣ ![]() ),
), ![]() (3﹣
(3﹣ ![]() ))
))
【解析】(1) 先通过直线解析式求AB求出坐标,再代入抛物线解析式 ;(2)设出P的坐标,用P的横坐标a表示其 纵坐标,再表示△POA的面积与△POB面积,按照题意列出关于a的方程;(3)利用对称法求两线段和最小值,A的对称点就是抛物线与x轴的另一个交点C,连接PC与对称轴相交即可求出Q点;(4)“以点O、B、M、N为顶点的四边形是平行四边形”可找出一对固定点,对它进行分类讨论: OB为平行四边形的边;OB为对角线,OB与MN互相平分;按照几何关系构建关于M的横坐标为未知数的方程求解.

 名校课堂系列答案
名校课堂系列答案